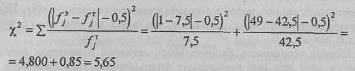Пример 2

В тренинге профессиональных наблюдателей допускается, чтобы наблюдатель ошибался в оценке возраста ребенка не более чем на 1 год в ту или иную сторону. Наблюдатель допускается к работе, если он совершает не более 15% ошибок, превышающих отклонение на 1 год. Наблюдатель Н допустил 1 ошибку в 50-ти попытках, а наблюдатель К - 15 ошибок в 50-ти попытках. Достоверно ли отличаются эти ре­зультаты от контрольной величины?

Определим частоту допустимых ошибок при п = 50:

f _теор=n· Р =50·0,15=7,5

Для наблюдателя Н f _эмп< f _теор. Для наблюдателя К f _эмп> f _теор

Сформулируем гипотезы для наблюдателя Н.

H₀: Количество ошибок у наблюдателя Н не меньше, чем это преду­смотрено заданной величиной.

H₁: Количество ошибок у наблюдателя Н меньше, чем это предусмот­рено заданной величиной.

В данном случае Р=0,15<0,50; f _эмп> f _теор.

Этот случай попадает под вариант Б Табл. 5. 12. Нам придется применить критерий у}, сопоставляя полученные эмпирические частоты ошибочных и правильных ответов с теоретическими частотами, состав­ляющими, соответственно, 7,5 для ошибочного ответа и (50-7,5)=42,5 для правильного ответа. Подсчитаем χ² по формуле, включающей по­правку на непрерывность[24]:

По Табл. IX Приложения 1 определяем критические значения χ² при v =l:

Ответ: H₀ отвергается. Количество ошибок у наблюдателя Н меньше, чем это предусмотрено заданной величиной (р≤0,05)

Сформулируем гипотезы для наблюдателя К.

H₀: Количество ошибок у наблюдателя К не больше, чем это преду­смотрено заданной величиной.

H₁: Количество ошибок у наблюдателя К больше, чем это предусмот­рено заданной величиной.

В данном случае Р=0,15<0,5; f _эмп> f _теор.Этот случай подпадает под вариант А Табл. 5.12. Мы можем применить биномиальный крите­рий, поскольку n=50.

По Табл. XV Приложения 1 определяем критические значения при п=50, Р=0,15, Q=0,85:

Ответ: H₀ отвергается. Количество ошибок у наблюдателя Н меньше, чем это предусмотрено заданной величиной (р<0,05).