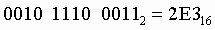Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Позиционные системы счисления Запись произвольного числа x в P-ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена x = a 0· pn + a 1· pn –1 +... + an –1· p 1 + an · p 0, где a 0... an – это цифры данного числа в системе счисления с основанием p. Примеры алфавитов нескольких систем:
основание системы приписывается нижним индексом к этому числу: 1011012 , 36718 , 3B8F16 Перевод целых чисел ü Перевод из десятичной системы счисления в другие Первый способ перевода 1. Число 2210 перевести в двоичную систему счисления.
2. Число 57110 перевести в восьмеричную систему счисления.
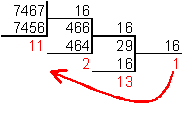
3. Число 746710перевести в шестнадцатеричную систему счисления.
Проверка: 1D2B16 =1*163+13(D)*162+2*161 +11(B) *160 = =4096 + 3328 + 32 +11 = 746710 Второй способ перевода Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 1).
Пример: Число 10010112 перевести в восьмеричную систему счисления.
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады, начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей цифрой (табл. 2).
Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления.
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример: Число 5318 перевести в двоичную систему счисления. 5318 = 101 011 0012
|