МЕТОДИЧЕСКАЯ РАЗРАБОТКА
Уч.год
Содержание Практические работы
 \ \
ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН
1 Цель работы
1.1 Повторить формулы для вычисления площадей плоских фигур; 1.2 Повторить формулы для вычисления объёмов геометрических тел; 1.3 Повторить правила выполнения действий с векторами
2 Ход работы Вариант 2.1 Вычислить площадь фигуры, изображённой на рисунке
b
2.2 Найдите площадь треугольника, вершины которого имеют координаты
A(a; b), B(m; n), C(d; b)
2.4 Вычислите площадь фигуры, изображённой на рисунке
2.5 Найти длины проекций вектора, модуль которого равен z на оси ОХ и ОУ, если вектор образует с осью ОХ угол α. Выполните рисунок.
3. Вывод
В ходе выполнения работы применены формулы:
ПРАКТИЧЕСКАЯ РАБОТА 2
Выполнение действий над комплексными числами
1.1. Научиться выполнять действия над комплексными числами.
2. Ход работы Вариант
2.1.1. Найдите значение выражения:
2.1.2. Найдите сумму, разность, произведение и частное чисел:
2.1.3. Записать число в тригонометрической форме и перевести его в алгебраическую форму, если: 2.1.4. Записать число в показательной форме и перевести его в алгебраическую форму, если: 2.1.5. Перевести число в тригонометрическую форму: 2.1.6. Перевести число в показательную форму: 2.1.7. Найти произведение и частное чисел 2.1.8. Найти
2.1. Допуск к работе
2.2.1. Что такое мнимая единица? ______________________________________________________________________
2.2.2. Какое число называется комплексным? ____________________________________________________________________________________________________________________________________________
2.2.3. Как обозначаются действительная и мнимая части комплексного числа? ____________________________________________________________________________________________________________________________________________
2.2.4. Какой вид имеет комплексное число в алгебраической форме?__________________
2.2.5. Как вычислить модуль комплексного числа
2.2.6. Какой вид имеет комплексное число в тригонометрической форме? ______________________________________________________________________
2.2.7. Какой вид имеет комплексное число в показательной форме? ______________________________________________________________________
2.2.8. ______________________________________________________________________
2.2.9. Формула извлечения корня степени п ________________________________
К работе допускается _______________
3. Выполнение работы
Исследование сложных функций и построение их графиков
1. Цель работы
1.1 Научиться применять производную для исследования функций. 1.2. Научиться определять и строить асимптоты графиков.
2. Ход работы Вариант
2.1. Уравнение вертикальной асимптоты _______________________________________
2.2. Формула производной сложной функции ___________________________________ 2.3. Точка х0 называется точкой минимума, если__________________________________ ___________________________________________________________________________ 2.4. Допишите правила
3 ВЫПОЛНЕНИЕ РАБОТЫ Исследовать функцию методами дифференциального исчисления, и используя результаты исследования, построить ее график
Решение прикладных задач на применение производной
1. Цель работы
1.1 Научиться применять геометрический и физический смысл производной для решения задач. 1.2 Научиться применять производную для исследования функций на монотонность и экстремумы. 1.3 Научиться применять производную второго порядка для исследования функций на выпуклость, вогнутость и точки перегиба. 1.4 Научиться применять производную для исследования функций на наибольшее и наименьшее значение на отрезке.
2. Ход работы Вариант
Первая производная от пути по времени равна …………………………… Вторая производная от пути по времени есть ……………………………. Уравнение касательной к графику у=f(х) в точке х0: Уравнение нормали: Если производная дифференцируемой функции положительна (отрицательна) на……. ……………………………………………………………………………………………………..
Алгоритм определения промежутков выпуклости и вогнутости графика функции 1. 2. 3. 4. Применить схемы
К работе допускается ______________ 2.1.Тело движется прямолинейно по закону Найти: а) скорость в момент времени t = c; б) момент времени, когда ускорение равно м/с2. 2.2.Составьте уравнение касательной и нормали к кривой
2.3.Исследуйте на монотонность и экстремумы функцию 2.4. Исследуйте на выпуклость, вогнутость и точки перегиба функцию
2.5. Найти наибольшее и наименьшее значения функции
Решение прикладных задач с помощью определённого интеграла
1. Цель работы 1.1 Научиться применять определённый интеграл для решения геометрических задач. 1.2 Научиться применять определённый интеграл для решения физических задач.
2. Ход работы Вариант
Геометрический смысл определённого интеграла: ________________________________ ______________________________________________________________________
Формула длины дуги плоской кривой___________________________________________
Формула объёма фигуры, полученной при вращении вокруг оси ____________________________________________________________________________
Физический смысл определённого интеграла: ____________________________________
Формула работы переменной силы: ____________________________________________
Формула вычисления силы давления жидкости на вертикально расположенную пластину: ___________________________________________________ К работе допускается ______________
1. Вычислить силу давления на прямоугольную пластину с основанием см и высотой см, погруженную вертикально в жидкость плотности ρ= 1510 кг/м3 так, что верхнее основание находится на см ниже поверхности жидкости. 2. Скорость движения тела задается формулой Найти путь пройденный телом за а) секунд; б) -ую секунду. 3. Силой H пружина растягивается на см. Первоначальная длина пружины равна см. Какую работу надо совершить, чтобы растянуть пружину до см? 4. Найти площадь фигуры, ограниченной линиями:. 5. Найти длину дуги кривой между точками х= и х=. 6. Найти объём тела, полученного при вращении кривой вокруг оси ОХ, если - ≤ х ≤.
3.Выполнение работы
ПРАКТИЧЕСКАЯ РАБОТА 6
Матрицы. Определители. Решение СЛАУ методами Крамера и Гаусса.
1. Цель работы
1.1. Научиться выполнять сложение матриц, умножение матриц на число, умножение матриц и вычислять определители. 1.2 Научиться решать СЛАУ по формулам Крамера и методом Гаусса.
2. Ход работы Вариант 1. Вычислите определитель второго порядка: 2. Вычислите определитель третьего порядка: 3. Решите системы уравнений, используя формулы Крамера:
5. Решить систему уравнений методом Гаусса:
2.2. Допуск к работе
2.2.1. Что называется матрицей? _________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.2. Что называется суммой матриц? _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.3. Как найти произведение двух матриц? __________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.4. Формула вычисления определителя матрицы второго порядка:
2.2.5.
3.Выполнение работы
ПРАКТИЧЕСКАЯ РАБОТА 7
Решение задач линейной алгебры
1. Цель работы
Научиться решать задачи линейной алгебры.
2. Ход работы Вариант
1. Даны матрицы: 2. Найти: сумму элементов второй строки матрицы А+5В- СТ;
3. Решить уравнение
4. Решить уравнение
2.2 Допуск к работе
1 Определение транспонированной матрицы__________________________________ _________________________________________________________________________ _________________________________________________________________________
2. Формула корней квадратного уравнения
3. Вычислить определители:
4. Решить уравнения:
3.Выполнение работы
Вычисление вероятности с использованием элементов комбинаторики и решение статистических задач.
1. Цель работы
1.1 Научиться применять определение вероятности и её свойства при решении задач. 1.2 Научиться составлять закон распределения и вычислять вероятности по условию задачи. 1.3 Научиться обрабатывать выборку.
2. Ход работы вариант kn
1. В урне белых и чёрных шаров. Из урны вынимают подряд 2 шара. Найти вероятность того, что 1) оба шара белые, 2) шары разного цвета. 2. Составить закон распределения случайной величины Х-число попаданий в цель при выстрелах, если вероятность попадания при одном выстреле равна 0.8. Изобразить графически закон распределения. Найти наиболее вероятное число попаданий. Найти наименее вероятное число попаданий. Определить вероятность того, что число попаданий а) больше; б) Не больше; в) от до. 3. Пусть дана выборка: k+2, k-2, k, k, 2k, 2k, k+3, k+2, k-1, k-1, k-2, 2k+1, k-10, 2k, k+10.Для данной выборки найти: а). объём; б). размах; в) моду, г) медиану. Записать выборку в виде вариационного ряда. Найти: 2.2 Допуск к работе Что называется многоугольником распределения?_____________________ _________________________________________________________________ ____ _____________________________________________________________ 1. Найти объём выборки 2,5,2,4,1,2,5,0,0,-1,-1,6,5,8,8. а). 15 б) 16 в) 7 г) 8 д) нет правильного ответа 2. Размах выборки 55,45,48,46,4,49,-2,0,13,-1,-1,5 равен: а). 53 б) 54 в) -55 г) 57 д) нет правильного ответа 3. Выборка -11,-11,-10,-4,0,3,3,3,4,15,15,20,20. записана в виде: а). статистического ряда б) вариационного ряда в) нет закономерности г) выборочного распределения. 4. Мода выборки равна 2, 5, 2, 4, 1, 2, 5, 0, 0,-1,-1,6,5,8,12, -2, 5, 0,2. а) 2; б) 5; в) 0; г) моды нет.
5. Вероятностью события А называется ……………………………………………………. ………………………………………………………………………………………………………………………………………………………………………………………………………… 3. Выполнение работы
3.1 А - Оба белые Р(А) =
В – разного цвета Р(В) =
Наиболее вероятное число попаданий: Наименее вероятное число попаданий:
Вероятность того, что число попаданий
а) больше;
б) Не больше;
в) от до 3.3 Объём n = размах h = моду = медиану Записать выборку в виде вариационного ряда
составить статистический ряд.
4. Вывод В ходе работы МЕТОДИЧЕСКАЯ РАЗРАБОТКА для студентов I курса фармацевтического факультета к практическому занятию по теме «Статистическая обработка данных с использованием пакета Statistica» 1. Научно-методическое обоснование темы: Эффективная работа специалиста-медика на сегодняшний день подразумевает знание не только медицинских дисциплин, но также и хорошее владение навыками автоматизированной обработки медицинских данных. Практически всем специалистам в области медицины необходим навык по осуществлению статистической обработки данных, которая должна производиться с применением современных программно-технических средств. Почти нет ни одной врачебной должности в больнице (в клинике), в поликлинике, занимая которую, врачу не пришлось бы выполнять какие-нибудь статистические работы. Поэтому, представляется важным, чтобы лечащие врачи знали, как взяться за дело, умели собирать и обрабатывать верные цифры, годные для сравнения и сопоставления. Не только врачи-клиницисты, но и врачи-экспериментаторы, врачи гигиенисты и организаторы здравоохранения не в меньшей мере нуждаются в умении правильно применять статистические методы исследования и правильно толковать и использовать результаты этих исследований. Материал данной методической разработки предназначен для изучения основ статистического анализа студентами медицинских вузов в рамках дисциплины «Медицинская информатика» с использованием пакета Statistica 6.0.
2. Краткая теория: Основные понятия и определения В самых различных областях (медицина, налоговая служба, экономика, геология и т.д.) объекты описываются набором величин, то есть являются многомерным. А обработка таких данных очень трудоемкая работа. Но в данном математическом пакете процесс анализа данных превращается в увлекательное исследование с использованием компьютерных технологий.
|

 ПРАКТИЧЕСКАЯ РАБОТА 1
ПРАКТИЧЕСКАЯ РАБОТА 1


 2.3 Найти площадь трапеции
2.3 Найти площадь трапеции
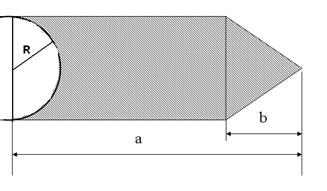


 Найти объём части цилиндра, изображённой на рисунке
Найти объём части цилиндра, изображённой на рисунке




 ,
, 
 ,
, 


 и
и  .
. ? _______________________
? _______________________ Какое комплексное число называется сопряжённым к комплексному числу
Какое комплексное число называется сопряжённым к комплексному числу  ПРАКТИЧЕСКАЯ РАБОТА 3
ПРАКТИЧЕСКАЯ РАБОТА 3
 ПРАКТИЧЕСКАЯ РАБОТА 4
ПРАКТИЧЕСКАЯ РАБОТА 4 …………
…………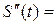 …………
………… Определить вид экстремума функции, если
Определить вид экстремума функции, если и
и 
 .
. в ее точке с абсциссой х0 =.
в ее точке с абсциссой х0 =. .
. ПРАКТИЧЕСКАЯ РАБОТА 5
ПРАКТИЧЕСКАЯ РАБОТА 5 кривой
кривой 






 ,
,  , АхВ
, АхВ

 Как вычислить определитель третьего порядка по схеме треугольников?
Как вычислить определитель третьего порядка по схеме треугольников? ;
;  ;
;  .
.



 ПРАКТИЧЕСКАЯ РАБОТА 8
ПРАКТИЧЕСКАЯ РАБОТА 8 ,
,  ,
,  .
.




