Формулы сокращенного умножения. Бином Ньютона.
Формулы сокращенного умножения. Бином Ньютона.
Выражения, составленные из чисел и переменных, связанных действиями сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, называются алгебраическими выражениями. При выполнении преобразований алгебраических выражений используются формулы сокращенного умножения:
Формулы квадрата и куба суммы являются частными случаями формулы бинома Ньютона, которая служит для возведения в натуральную степень суммы двух слагаемых: где Формула бинома Ньютона обладает следующими свойствами: 1) в разложении двучлена 2) сумма показателей степеней a и b в каждом члене равна n; 3) биномиальные коэффициенты членов, равноудаленных от концов разложения, равны между собой; 4) сумма биномиальных коэффициентов разложения Биномиальные коэффициенты можно вычислять, используя схему, которая называется треугольником Паскаля.
Найти (к+1) – й член разложения можно по формуле: ---------------------------------------------------------------------------------------------------------------- Бином Ньютона. Стр 1. Пример 1. Разложить выражение Решение. Разложение будет иметь вид:
Пример 2. Сумма биномиальных коэффициентов разложения Решение. По свойству 4) бинома Ньютона Т.к n=3m, то m=2. Следовательно имеем разложение Слагаемое не содержит х в том случае, если степень х равна нулю. Воспользуемся формулой (к+1) – го члена разложения:
Составим уравнение для определения номера члена разложения: 6 – 3k = 0 Значит,
|
– квадрат суммы;
– квадрат разности;
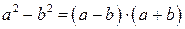– разность квадратов;
– куб суммы;
– куб разности;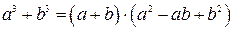
– сумма кубов;
– разность кубов.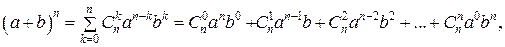
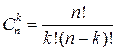– биномиальные коэффициенты.
по формуле Ньютона содержится n+1 член;
;
.
по формуле бинома Ньютона.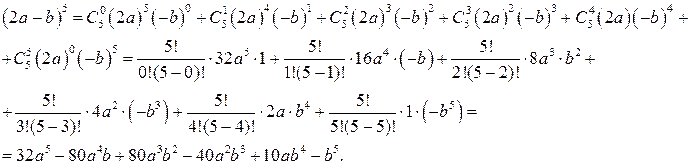
равна 64. Определить слагаемое, не содержащее x.
.
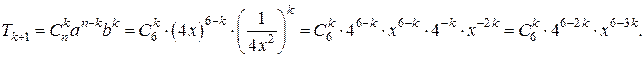
k = 2.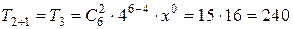
.
