Оптимальное распределение полюсов системы управления
Оптимальное распределение полюсов системы управления При описании объекта управления с помощью векторно-матричной модели в пространстве состояний первый способ задания качества управления может быть трансформирован в оптимальное распределение на комплексной плоскости полюсов замкнутой системы. Для системы, описываемой векторно-матричной моделью в непрерывном времени
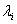 (A), где i =1, 2,..., n. В то же время собственными значениями матрицы А называются корни ее характеристического уравнения (A), где i =1, 2,..., n. В то же время собственными значениями матрицы А называются корни ее характеристического уравнения
Расположение полюсов на комплексной плоскости во многом характеризует синтезируемую систему, определяя ее переходные и частотные характеристики, а, следовательно, и динамические показатели качества. Так, например, устойчивость системы определяется размещением полюсов в левой полуплоскости. Наличие нулей в замкнутой системе в определенной степени влияет на ее динамику. Синтезу регуляторов состояния предшествует решение задачи построения эталонной модели системы управления, которая соответствует желаемому распределению на комплексной плоскости корней характеристического уравнения A(s) = 0 замкнутой системы. Если все составляющие вектора состояния объекта могут быть измерены (имеется полная информация о векторе состояния), то обеспечение заданного расположения корней не вызывает трудностей. В этом случае возникает вопрос о том, какое расположение корней выбрать. Если передаточная функция замкнутой системы не имеет нулей, то при выборе ее желаемого полинома A(s) можно руководствоваться стандартными формами (фильтрами), которые нашли достаточно широкое применение на практике. Стандартные формы определяют коэффициенты характеристического полинома (знаменателя) функции Н(s), обеспечивающие в системе переходные и частотные характеристики с известными показателями качества. Если же система характеризуется наличием нулей, стандартные формы могут служить в качестве исходного материала для поиска своего оптимального расположения корней. Как правило, в характеристическом полиноме сначала выделяются полюса для компенсации нулей, а оставшийся полином формируется из условия желаемого расположения корней. В табл. 6.1 и 6.2 приводятся формулы характеристического полинома и соответствующие им коэффициенты для некоторых наиболее распространенных на практике распределений:/
Качество работы системы управления характеризуется, с одной стороны, ее точностью в установившемся режиме, а c другой - переходным процессом от одного установившегося состояния к другому. При исследовании переходных процессов чаще всего полагают, что входной сигнал является единичной ступенчатой функцией. В этом случае кривая переходного процесса называется переходной функцией и характеризуется некоторыми показателями, принимаемыми за меру качества системы управления. К числу таких показателей могут быть отнесены (рис. 6.1):
Типовые переходные характеристики для различных фильтров при входном ступенчатом сигнале качественно представлены на рис.
|


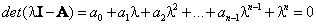



 ;
;


