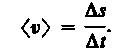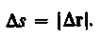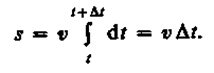Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор г0 (рис. 3). В течение малого промежутка времени Dt точка пройдет путь Ds и получит элементарное (бесконечно малое) перемещение Dг.
Рис. 3
Вектором средней скорости <v> называется отношение приращения Dг радиуса-вектора точки к промежутку времени Dt:
(2.1) Направление вектора средней скорости совпадает с направлением Dг. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dг|, поэтому модуль мгновенной скорости
Таким образом, модуль мгновенной скорости равен первой производной пути по времени:
При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной <v> — средней скоростью неравномерного движения:
Из рис. 3 вытекает, что <v> > |<r>|, так как Ds >|Dг|, и только в случае прямолинейного движения
Если выражение ds=vdt (см. формулу (2.2)) проинтегрировать по времени в пределах от t до t+ Dt, то найдем длину пути, пройденного точкой за время Dt:
(2.3) В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид
Длина пути, пройденного точкой за промежуток времени от t\ до fa, дается интегралом
|



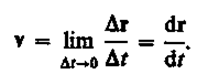

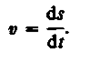 (2.2)
(2.2)