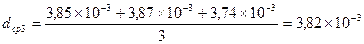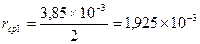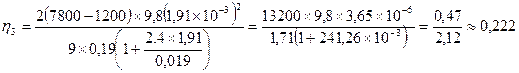Министерство образования и науки Российской федерации. Лабораторная работа На тему: “Определение коэффициента вязкости жидкости по методу Стокса”.
Лабораторная работа
21040165 09М 911 Шифр Номер работы Группа
Черных Д. С. Проверил: Бодров Е. А.
Цель работы: Определение коэффициента вязкости касторового масла; вычисление числа Рейнольдса; определение времени релаксации.
Приборы и оборудование: 1. Стеклянный цилиндрический сосуд с касторовым маслом 2. Электрический секундомер 3. Стальные или свинцовые шарики 4. Микрометр и масштабная линейка Краткая теория: Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твердым, поэтому она обладает свойством как газообразных, так и твердых тел. Жидкости, подобно твердым телам, обладают определенным объемом, а также принимают форму сосуда, в котором находятся, подобно газам. Молекулы газа занимают предоставленный им объем, так как практически отсутствуют силы межмолекулярного взаимодействия и средняя кинетическая энергия теплового движения молекул газа гораздо больше средней потенциальной энергии, обусловленной силами притяжения между ними. Вследствие этого молекулы газа разлетаются, и газ занимает предоставленный ему объем сосуда. В твердых и жидких телах силы притяжения между молекулами уже существенны и удерживают молекулы на определенном расстоянии друг от друга. Средняя кинетическая энергия теплового движения молекул меньше средней потенциальной энергии обусловленной силами межмолекулярного взаимодействия, поэтому ее недостаточно для преодоления сил притяжения между молекулами, в результате чего твердые тела и жидкости имеют определенный объем. Следует отметить, что в газах молекулы двигаются хаотично и не имеют четко определенного местоположения, в твердых телах существует так называемый дальний порядок (упорядоченность в расположении молекул, повторяющаяся на больших расстояниях), что касается жидкостей, то в них дальний порядок нарушается, но молекулы движутся не полностью хаотично, а в ближнем порядке (упорядоченность в расположении молекул, повторяющаяся на расстояниях, сравнимых с межмолекулярными). Кроме того, по теории Френкеля, тепловое движение в жидкости объясняется тем, что каждая молекула в течение некоторого времени колеблется на одном месте, после чего скачком переходят в новое положение, находящееся приблизительно на одно межмолекулярное расстояние от прежнего. Таким образом, молекулы жидкости довольно медленно перемещаются по ее массе. С повышением температуры частота колебательного движения резко увеличивается, возрастает подвижность молекул. В жидкостях, подобно газам, наблюдаются явления переноса: диффузия, теплопроводность и вязкость. Остановимся на последнем. Вязкость жидкости – это перенос импульса от слоя к слою, текущей, например, по трубе жидкости. При течении жидкости по трубе различные слои имеют разные скорости. Наибольшая скорость наблюдается у центрального слоя. Если перпендикулярно векторам скорости провести ось Х, то можно пронаблюдать градиент скорости, образованный этими векторами. Перенос импульса вызывает движение слоев, т. е. начинает действовать сила, равная Характерным для жидкостей является сильная зависимость В жидкостях наблюдается два вида течений: ламинарное и турбулентное. При ламинарном течении жидкость течет слоями, которые скользят друг относительно друга и при этом не перемешиваются. Такое течение считается стационарным. Если же увеличивать скорость или поперечные размеры потока жидкости возникает ее перемешивание. Скорость молекул в любом месте все время беспорядочно меняется, то течение считается нестационарным и называется турбулентным. Ученый Рейнольдс установил, что характер течение жидкости зависит от безразмерной величины Расчетные формулы:
Проведем соответствующие расчеты и измерения:
Систематизируем результаты в виде таблицы:
Вывод: Выполнив данную лабораторную работу, я провел эксперимент, состоящий из трех опытов, в ходе которых я определил для каждого опыта: коэффициент вязкости жидкости (касторового масла) по методу Стокса, рассчитал число Рейнольдса и время релаксации. Я ознакомился с принципами, по которым можно определить коэффициент вязкости жидкости и число Рейнольдса, а именно с разновидностями внутренних течений и зависимостью вышеназванных величин от них. Отмечу, что в данной работе я наблюдал исключительно ламинарные течения – об этом говорит число Рейнольдса варьирующее от 1,96 до 2,87. В качестве измерительных приборов и оборудования мною были использованы: микрометр, линейка, секундомер, стальные шарики, цилиндр с одной подвижной и одной неподвижной меткой наполненный касторовым маслом. Министерство образования и науки Российской федерации
|

 , где
, где  - коэффициент вязкости.
- коэффициент вязкости. .
. 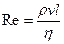 , где
, где  - плотность жидкости;
- плотность жидкости;  - средняя скорость потока;
- средняя скорость потока;  - характерный для поперечного сечения сосуда размер;
- характерный для поперечного сечения сосуда размер;  - средний диаметр шариков
- средний диаметр шариков - средний радиус шариков
- средний радиус шариков - скорость установившегося движения шарика
- скорость установившегося движения шарика - коэффициент вязкости жидкости
- коэффициент вязкости жидкости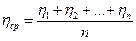 - средний коэффициент вязкости
- средний коэффициент вязкости - число Рейнольдса
- число Рейнольдса - время релаксации
- время релаксации