для экономических специальностей заочной формы обучения. Задание 1. Вычислить неопределенные интегралы: а
Вариант A Задание 1. Вычислить неопределенные интегралы:
Решение. а) При вычислении данного интеграла, сделаем подстановку t =5–9ln x, в результате получим
б) При вычислении данного интеграла, сделаем подстановку t =5+4 x 10, в результате получим
в) При вычислении данного интеграла воспользуемся формулой интегрирования по частям
Тогда получим
г) При вычислении данного интеграла также воспользуемся формулой интегрирования по частям. В результате получим
д) Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:
Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:
Чтобы найти неопределенные коэффициенты A, B, C, придадим переменной x три каких-либо значения (обычно выбирают такие значения, чтобы получались нулевые значения в правой части):
Таким образом,
Далее, вычисляем исходный интеграл
е) Для вычисления исходного интеграла применим тригонометрические формулы:
Тогда получим
Задание 2. Вычислить определенные интегралы:
Решение. а) При вычислении данного интеграла, преобразуем подынтегральное выражение
б) При вычислении данного интеграла применим метод замены переменной (обратим внимание, что в определенных интегралах, кроме подынтегрального выражения, преобразуются также и пределы интегрирования):
в) При вычислении данного интеграла применим метод интегрирования по частям:
Задание 3. а) В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара. б) Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные? Решение. Вспомним классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:
Вероятность P (A) события А должна удовлетворять следующим условиям: 1о. P (A)=1, если А – достоверное событие; 2о. P (A)=0, если А – невозможное событие; 3о. 0< P (A)<1, если А – случайное событие. Для подсчета вероятностей по классической формуле обычно используют методы комбинаторики. Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов в соответствии с каким-либо правилом. Существует две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов. Это означает, что в выборке невозможны повторения элементов. Во второй схеме выбор осуществляется по-элементно с обязательным возвращением отобранного элемента при каждом шаге. Это означает, что в выборке возможны повторения. После того, как выбор тем или иным способом осуществлен, отобранные элементы могут быть либо упорядочены, либо неупорядочены. В первом случае, выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки объявляются тождественными.
а) Поскольку в данной задаче неважен порядок, то для решения будем применять сочетания без повторения (шары не возвращаются обратно в урну). Найдем общее число возможных исходов:
Теперь найдем число благоприятствующих возможных исходов. Два белых шара можно вынуть m 1= C 22=1 способом, два разных цветных шара m 2= C 31× C 51=3×5=15 способами. Тогда общее число благоприятствующих исходов, в соответствии с принципом сложения, равно m = m 1+ m 2 = 16. Таким образом,
б) Всего имеется 10 цифр. Поскольку при составлении пятизначным номеров важен порядок и возможны повторения, то общее число возможных пятизначных номеров будет равно
Номера, у которых все цифры разные, – это размещения без повторений
Таким образом, искомая вероятность равна
Задание 4. а) В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара. б) Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные? Решение. Вспомним теоремы сложения и умножения вероятностей: Теорема сложения вероятностей несовместных событий. P (A+B) = P (A) + P (B). Теорема сложения вероятностей совместных событий. P (A+B) = P (A)+ P (B)– P (AB). Теорема умножения вероятностей независимых событий. P (AB) = P (A) P (B). Теорема умножения вероятностей зависимых событий. P (AB) = P (A) PA (B) = P (B) PB (A). Достоверное событием обычно обозначается символом W, невозможное событие – символом Æ. Тогда
а) Пусть событие В состоит в том, что выстрел произошел, тогда событие P (AB) = P (B) PB (A) = 0б98×0б8 = 0б784. б) Пусть A 1={первый стрелок попал по цели}, A 2={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А 1+ А 2. Поскольку события А 1 и А 2 совместны, но независимы, то P(А 1+ А 2) = P (А 1)+ P (А 2)– P (А 1) P (А 2) = 0,7+0,8–0,7×0,8 = 0,94. Отметим, что событие В можно записать также в виде P (B) = P (A 1) P ( Задание 5. а) Вероятность изготовления на станке-автомате нестандартной детали равна 0,02. Какова вероятность того, что среди наудачу взятых шести деталей окажется более четырех стандартных? б) Вероятность того, что сошедшая с конвейера деталь стандартная равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей: 1) 356 окажутся стандартными; 2) более 350 деталей окажутся стандартными. Решение. а) Проведем n испытаний Бернулли, т.е. что все n испытаний независимы и вероятность появления события А в каждом отдельном взятом испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность P (A) появлений события А в отдельном испытании буквой p, т.е. P (A)= p, а вероятность противоположного события P (
Это есть формула Бернулли. По условию задачи, вероятность того, что наудачу взятое изделие окажется нестандартным равна q =0,02. Вероятность того, что изделие окажется стандартным равна p= 1– q =0,98. Поскольку эти вероятности постоянны и не изменяются от испытания к испытанию, то для подсчета вероятности можно применить формулу Бернулли. Появление более четырех стандартных изделий означает, что среди 6 взятых деталей окажутся 5 или 6 стандартных. Следовательно
= 5×0,985×0,021 + 1×0,986×0,020» 0,9943. б) Применим к случаю 1 локальную теорему Муавра-Лапласа: если в схеме Бернулли число испытаний n велико (обычно nt50), при этом npq ‡1, то справедлива приближенная формула
где Ввиду важности функции j(x), которая называется плотностью стандартного нормального распределения, для нее составлены специальные таблицы. При использовании таблиц следует учитывать, что функция j(x) четная, т.е. j(– x)=j(x). Согласно условию задачи: n =400, m =356, p =0,9, q =0,1. Поскольку n >100 и npq =36>10, то можно применить теорему Муавра-Лапласа. Найдем
После этого находим значение функции j(–0,6667)=0,31945. В результате, получаем
Применим теперь к случаю 2 интегральную теорему Муавра-Лапласа: если в схеме Бернулли число испытаний n велико, то для вероятности P n (k 1£ m £ k 2) того, что число успехов заключено в пределах от k 1 до k 2, справедливо приближенная формула
где Отметим, что функция Лапласа – нечетная функция, т.е. Ф(– x) = –Ф(x), для которой составлены специальные таблицы. Обратите внимание, что 0£Ф(x)£0,5. В нашем случае k 1=300, k 2=400:
Задание 6. Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того, что Х примет значение x 1 равно 0,6. Найти закон распределения Х, зная математическое ожидание М[ X ] = 1,4 и дисперсию D[ X ] = 0,24. Решение. Сумма вероятностей всех возможных значений X равна единице, поэтому вероятность того p 2, что X примет значение x 2, равна 1–0,6=0,4. Запишем закон распределения дискретной случайной величины X:
Для отыскания x 1 и x 2 составим два уравнения. По определению M[ X ] = Учитывая, что по условию М[ X ] = 1,4, запишем первое из уравнений:
Принимая во внимание, что по условию D[ X ] = 0,24, и используя равенство
напишем второе уравнение:
В результате получается следующая система уравнений:
Выразив x 1 из первого уравнения и подставив его во второе, получим квадратное уравнение
Отсюда находим два решения:
Задание 7. Непрерывная случайная величина Х задана функцией распределения.
Решение. Найдем плотность распределения f (x)= F' (x):
Параметр k определим из условия
В нашем случае
Таким образом, плотность распределения имеет вид
Найдем теперь математическое ожидание
Найдем теперь дисперсию, для этого предварительно вычислим
Тогда
Задание 8. Известны математическое ожидание а =165 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал Решение. Плотность функции нормального распределения имеет вид:
Функция нормального распределения имеет вид
Однако часто вместо функции нормального распределения используется функция Лапласа F(x):
где а) Вероятность того случайная величина X, описываемая нормальным распределением, примет значение, принадлежащее интервалу (a,b), имеет вид
В нашем случае получим
б) Вероятность того, что отклонение случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа d, вычисляется по формуле:
В нашем случае получим
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
|




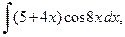


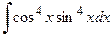 .
.

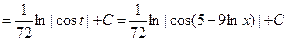 .
.
 .
. .
.
 .
.
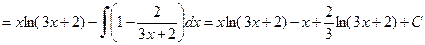 .
. .
.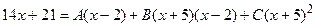 .
.
 .
.
 .
.
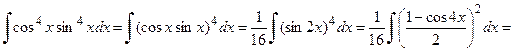

 .
.

 .
.

 .
.
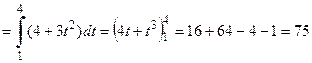 .
.

 .
.
 Набор
Выбор
Набор
Выбор






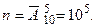


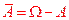
 означает противоположное событие, т.е. что произошла осечка. По условию P (
означает противоположное событие, т.е. что произошла осечка. По условию P ( . Тогда получим
. Тогда получим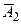 )+P(
)+P( )P(A 2)+ P (A 1) P (A 2) == 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.
)P(A 2)+ P (A 1) P (A 2) == 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94. ) – буквой q, т.е. P (
) – буквой q, т.е. P ( .
.
 ,
,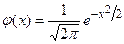 ,
,  .
. .
. .
. ,
, ,
,  – функция Лапласа.
– функция Лапласа.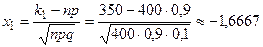 ,
,  ,
,
 = x 1 p 1+ x 2 p 2+... + xnpn.
= x 1 p 1+ x 2 p 2+... + xnpn. .
. ,
, , или
, или  .
.
 .
. и
и  (отсюда получаем также, что
(отсюда получаем также, что  и
и  ). По условию
). По условию  , поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид
, поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид

 .
. .
.

 .
.
 .
. .
. .
.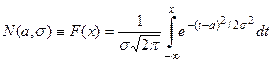 .
. ,
, – функция Лапласа.
– функция Лапласа.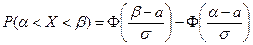 .
.
 .
.

 ,
,
 ,
,
 , a ¹1,
, a ¹1,
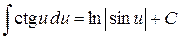 ,
,
 ,
,
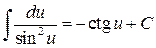 ,
,
 ,
,
 ,
,
 ,
,
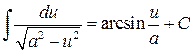 ,
,
 ,
,
 ,
,
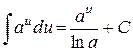 ,
,
 ,
,
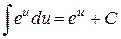 ,
,
 ,
,
 ,
,
 ,
,
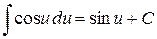 ,
,
 .
.



