Понятие функции
Пусть Х и У – некоторые множества. Опр. Если каждому элементу
Множество Х называется областью определения функции и обозначается D(f), множество У называется областью значений функции и обозначается I(f). В мат. анализе рассматривают в основном числовые функции, т.е. такие, где Х и У – множества действительных чисел.
Если функция f переводит элемент
Способы задания функций (задать множества и описать правило): - аналитический, с помощью одной или нескольких формул:
- табличный:
- графический (ЭКГ); - словесный (функция Дирихле 1-рац., 0-иррац.);
Например,
Функция называется явной, если она задана формулой, разрешенной относительно зависимой переменной. Если функция задана уравнением, не разрешенным относительно зависимой переменной, то говорят, что функция задана неявно. (
Опр. Композицией отображений Например,
Композицию числовых функций называют сложной функцией или функцией от функции.
Опр. Если обратное соответствие, переводящее Y в X является функцией, т.е. у каждого элемента
Пример. Рассмотрим функцию Выразим х: Т.к. традиционно независимую переменную обозначают х, то, переобозначив переменные, получим обратную функцию
Обратная функция к обратной функции совпадает с исходной функцией: Обратная функция существует для любой строго монотонной функции.
Опр. Графиком числовой функции y=f(x) называется совокупность точек плоскости вида (x,f(x)), где Графики обратных функций симметричны относительно биссектрисы I и III координатных углов.
Некоторые свойства функций.
Опр. Числовая функция y=f(x) называется монотонно возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции:
Опр. Числовая функция y=f(x) называется ограниченной сверху на множестве А, если найдется число М такое, что:
Опр. Числовая функция y=f(x) называется ограниченной снизу на множестве А, если найдется число М такое, что:
Опр. Числовая функция y=f(x) называется ограниченной на множестве А, если найдется число К такое, что:
В противном случае функция называется неограниченной.
Примеры: Самостоятельно: вспомнить свойства периодичности, четности.
Элементарные функции и их классификация.
К основным элементарным функциям относят: линейную, степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции. Опр. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и/или конечного числа операций образования сложной функции, называются элементарными. Пример. Неэлементарные: Элементарные функции делят на алгебраические и трансцендентные. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий (например, полином, дробно-рациональная функция, иррациональная функция). Остальные – трансцендентные (показательная, логарифмическая, тригонометрические и обратные тригонометрические функции).
Знать свойства и графики основных элементарных функций. Повторить преобразования графиков функций.
Применение функций в экономике
Функции находят широкое применение в экономической теории и практике. Наиболее часто используются: - функция полезности (функция предпочтений) – зависимость эффекта некоторого действия от интенсивности этого действия; - производственная функция – зависимость результата производственной деятельности от обуславливающих факторов; в том числе: функции выпуска, издержек и т.п. - функции спроса, потребления, предложения – зависимость объема от различных факторов (цены, дохода и т.д.). Поскольку экономические процессы в реальности обусловлены рядом факторов, при их исследовании применяют функции нескольких переменных.
|

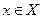 ставится в соответствие по некоторому правилу единственный элемент
ставится в соответствие по некоторому правилу единственный элемент 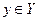 , то говорят, что на множестве Х задана функция (функциональная зависимость) со значениями в множестве У:
, то говорят, что на множестве Х задана функция (функциональная зависимость) со значениями в множестве У: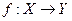 ,
, 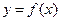 .
.
 - (читается «у равно антье х») целая часть – наибольшее число, не превосходящее х.
- (читается «у равно антье х») целая часть – наибольшее число, не превосходящее х. .
. )
) называется отображение
называется отображение  .
.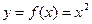 ;
; ;
; .
. ,
, 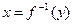 .
.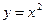 при x
при x  0.
0.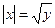 ,
,  . Обратной функцией будет являться
. Обратной функцией будет являться  .
. .
. .
.
 .
. .
.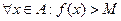 .
. .
. ,
,  .
.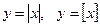 .
.


