Парная регрессия и корреляция
По северо-западному федеральному округу известны данные за 2001 г.
Задание: 1. Провести эконометрический анализ данных о среднедушевых денежных доходах и расходах населения регионов РФ. 2. Построить гистограмму, сделать содержательные выводы. 3. Построить диаграмму рассеивания, определить коэффициент корреляции между Х и Y, сделать вывод. 4. Вынести на диаграмму уравнение и значение коэффициента детерминации. 5. Определить параметры линейной регрессионной модели. Записать уравнение регрессии. 6. Проверить адекватность модели и провести интерпретацию уравнения регрессии. 7. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом 8. Оцените с помощью средней ошибки аппроксимации качество уравнения 9. Определить предсказанное значение Y, вычислить остатки. Построить график остатков, интерпретировать полученный результат.
Решение: Наибольшие среднедушевые доходы у населения Мурманской области, наименьшие - в Псковской. Наибольшие среднедушевые расходы в Санкт-Петербурге, наименьшие - в Псковской области. В Калининградской области и в Санкт-Петербурге среднедушевые денежные расходы превышают доходы, что может свидетельствовать о существовании теневых доходов населения.
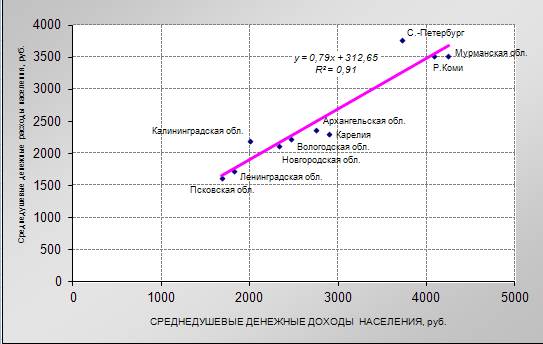
Рис.1 – Среднедушевые денежные доходы и среднедушевые расходы населения СЗФО, руб. Диаграмма рассеивания представлена на рис.2 (ромбы). Визуально - линейная зависимость между переменными существует. Нулевая гипотеза, Н0: изменение среднедушевых доходов не влияет на среднедушевые расходы населения,т.е.коэффициент регрессии равен 0. Альтернативная гипотеза, Н1: изменение среднедушевых доходов влияет на среднедушевые расходы населения, т.е.коэффициент регрессии не равен 0.
Уравнение регрессии строится с помощью опции "Добавить линию тренда", возникающей при выделении точек на диаграмме и нажатии правой кнопки. Уравнение для оценки регрессионной модели имеет вид: Y=312.65+0.79*Х. Величина коэффициента регрессии b=0,79 означает, что При приросте среднедушевых денежных доходов населения на 100 рублей можно ожидать возрастания среднедушевых расходов на 79 рублей. Коэффициент корреляции между Х и Y r = 0.95, что свидетельствует о наличии линейной зависимости между Х и Y.
Рис. 2 – Регрессионная зависимость между доходами и расходами населения Рассчитаем параметры a и b и сравним полученные результаты с уравнением тренда на графике. Параметры рассчитываются в результате решения системы нормальных уравнений относительно a и b.
Для оценки тесноты связи рассчитаем линейный коэффициент парной корреляции:
r 2YX = 0,952 = 0,9086 Коэффициент детерминации, равный 0,9086, устанавливает, что вариация потребительских расходов на душу населения на 90,86% из 100% предопределена вариацией средней заработной платы и выплат социального характера; роль прочих факторов, влияющих на потребительские расходы на душу населения, определяется в 9,14%, что является значительной величиной. Относительную оценку силы связи даёт общий (средний) коэффициент эластичности:
Для линейной регрессии формула принимает вид:
Это означает, что при изменении средней заработной платы и выплат социального характера на 1% от своей средней потребительские расходы на душу населения увеличивается на 0,877% от своей средней. Определим теоретические значения результата Yтеор. Для этого в полученное уравнение последовательно подставим фактические значения фактора X. Оценку качества модели дадим с помощью скорректированной средней ошибки аппроксимации ε'ср:
Значение величины скорректированной средней ошибки аппроксимации свидетельствует о не высоком качестве построенной линейной модели, но оно не ограничивает ее использование для выполнения точных прогнозных расчетов.
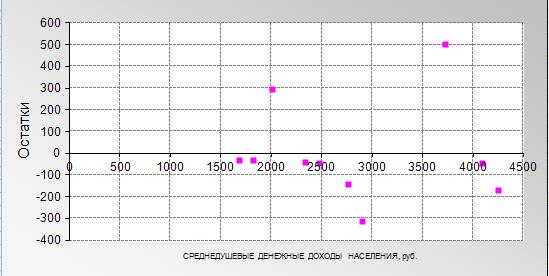
Рис. 3 – График остатков. Остатки гомоскедастичны, автокорреляции нет.
Критерий Фишера F = 79.5, значимость критерия Фишера 0.00001983<0.05, следовательно, в результате F-теста мы должны отклонить нулевую гипотезу и признать справедливость альтернативной гипотезы.
Р-значение=0.0000198<0.05, следовательно при уровне значимости, равном 0.05 нулевая гипотеза может быть отвергнута. Справедлива гипотеза о регрессионной зависимости между переменными. Доверительный интервал: 0.59<b<1.00
|


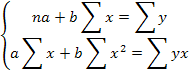
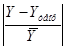
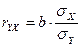 = 0,79*(930,08/775,47) = 0,95 что означает достаточно тесную связь между рассматриваемыми признаками.
= 0,79*(930,08/775,47) = 0,95 что означает достаточно тесную связь между рассматриваемыми признаками.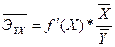
 = 0,79*(2803/2540) = 0,877
= 0,79*(2803/2540) = 0,877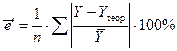 = (1/10*1)*100% = 10%
= (1/10*1)*100% = 10%