Решение типовых задач
ПОКАЗАТЕЛИ ВАРИАЦИИ (КОЛЕБЛЕМОСТИ) ПРИЗНАКА Виды дисперсии Решение типовых задач 4.4.1. Рассчитать показатели вариации для дискретного ряда (не сгруппированных данных), если известна выработка двух бригад строителей по одному виду продукции. Данные представлены во вспомогательной таблице 4.1. Таблица 4.1.
Решение: а) Абсолютные показатели вариации: Размах вариации:
Отклонение крайних вариант выработки в I бригаде на две детали выше, чем во второй (16-14). Для нахождения остальных показателей вариации необходимо найти среднюю выработку по каждой бригаде. Определяем среднею выработку по средней арифметической простой.
среднее линейное отклонение:
Степень рассеивания признаков в I бригаде выше чем II-й. Дисперсия (средний квадрат отклонений) и среднее квадратическое отклонение для не сгруппированных данных рассчитываются по следующим формулам:
Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Соотношение б) Относительные показатели вариации: - коэффициент осцилляции или относительный размах вариации: Колеблемость крайних показателей выработки вокруг средней в I бригаде больше чем во II-й. - Линейный коэффициент вариации (относительное линейное отклонение): Доля усредненных значений абсолютных отклонений от средней в I-й бригаде выше чем во II-й бригаде, на четыре процента (21-17). - Коэффициент вариации: Так как коэффициент вариации < 33% совокупности считаются однородными. в) Расчет показателей вариации для интервального вариационного ряда представлен в таблице 4.2. 4.4.2. Имеется распределение предприятии по объему выпуска продукции: Таблица 4.2
Решение: 1) 2) 3) 4) 5) Следовательно, вариация групп предприятий по выпуску продукции не однородная, т.к. коэффициент вариации больше 33% и составляет 45,4 %.
4.4.3. По двум цехам известны разряд и число рабочих. Дать квалификационную характеристику рабочих и рассчитать средний тарифный разряд. Показать правило сложений дисперсий найти все виды дисперсий. Таблица 4.3.
Решение: 1. Для квалификационной характеристики состава рабочих необходимо найти средний тарифный разряд для каждой бригады и общий по двум бригадам: 2. Рассчитаем общую дисперсию:
3. Рассчитаем групповую дисперсию:
4. Рассчитаем групповую дисперсию по второму цеху:
5. Рассчитаем среднюю из групповых дисперсий:
Таким образом средний тарифный разряд колеблется по I-му цеху – 2,125; по II-му цеху – 1,633; по обоим цехам вместе: 1,87. 6. Оценим колеблемость признака через межгрупповую дисперсию:
Итак, колеблемость групповых средних по сравнению с общей равна 0,23. Для проверки правильности выбранного решения используем правило сложения дисперсии: сумма межгрупповых дисперсий и средней из групповых равна общей дисперсии.
|


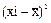
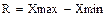
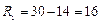 деталей;
деталей;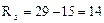 деталей.
деталей.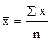 ;
;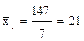 деталь;
деталь; детали;
детали;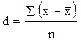 ;
;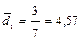 деталей;
деталей; деталей.
деталей. ;
;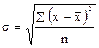 ;
;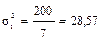 деталей;
деталей;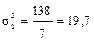 деталей;
деталей;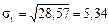 деталей;
деталей; детали.
детали.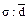 для нормального закона распределения должно равняться примерно 1:2. В задаче соотношение
для нормального закона распределения должно равняться примерно 1:2. В задаче соотношение 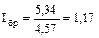 ;
;  . Следовательно, резких выделяющихся отклонений не однородных с основной массой элементов не наблюдается.
. Следовательно, резких выделяющихся отклонений не однородных с основной массой элементов не наблюдается.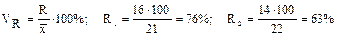 .
.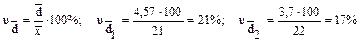 .
.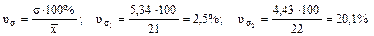 .
.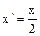
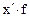
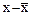

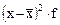
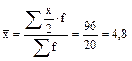 млн. руб.
млн. руб.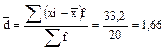 млн. руб.
млн. руб.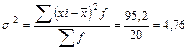 млн. руб.
млн. руб.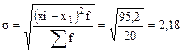 млн. руб.
млн. руб.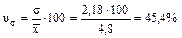
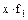
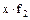
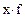
 .
.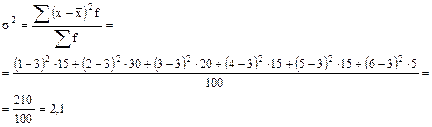
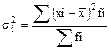
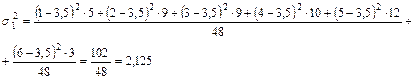
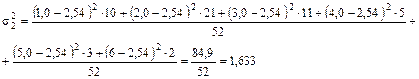
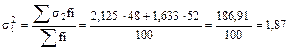
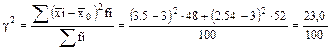
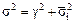 ;
; 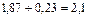 , что подтверждает правильность решения.
, что подтверждает правильность решения.


