Сжатие речевого сигнала
Модифицируем алгоритм, описанный в предыдущей главе, для сжатия речевого сигнала посредством ДИКМ. Для этого записанный отрезок речи подвергнем дискретизации с частотой Значения разностного сигнала, полученного при использовании оптимальных коэффициентов, можно записать при помощи 9-10 бит. Очевидно, что такое сжатие разностного сигнала является недостаточным, а следовательно, необходимо подвергнуть разностный сигнал дальнейшей обработке. Для этого будем еще раз квантовать сигнал, чтобы была возможность записать его при помощи 6 бит. На приемной стороне умножим полученный отсчет на использованный шаг квантования и продолжим алгоритм, как и в предыдущей главе.
Листинг соответствующей программы представлен ниже:
clear all; Fs=8000; t=0.5; a1=1.8; a2=-0.8;
beep x = wavrecord(t*Fs, Fs); [x1,sh,kvbin,x]=DAC(x,Fs,t,12,2); beep; wavplay(x*sh, Fs); %mu=255; %koef=32;
%beep; %wavplay(x*sh, Fs); q = fft(x,Fs*t); q = q(1:(Fs*t/2)); m = abs(q); m1=m/(Fs*t/2); f = (0:((Fs*t)-1)/2)/t;
tm=0:1/Fs:t; tm=tm(1:Fs*t);%
for n=1:Fs*t if n==1 pr_x(n)=0; elseif n==2 pr_x(n)=round((a1*x(n-1))); else pr_x(n)=round(((a1*x(n-1)+a2*x(n-2)))); end
end for n=1:Fs*t if n==1 e(n)=x(n); else e(n)=x(n)-pr_x(n); end
end e2=e; ma=max(abs(e)); [x1,sh_e,kvbin,e]=DAC(e,Fs,t,6,2); %for n=1:Fs*t %e(n)=round((sign(e(n))*koef*((log(1+mu*abs(e(n)/ma)))/(log(mu+1))))); %end
e1=e; %for n=1:Fs*t % e(n)=round(sign(e(n))*(1/255)*((256^(abs(e(n)/koef))-1))*ma); %end e=round(e*sh_e);
for n=1:Fs*t if n==1 y(n)=e(n); pr_y(n)=0; elseif n==2 pr_y(n)=round((a1*y(n-1))); y(n)=e(n)+pr_y(n); else pr_y(n)=round(((a1*y(n-1)+a2*y(n-2)))); y(n)=e(n)+pr_y(n); end
end
w = fft(e,Fs*t); w = w(1:(Fs*t/2)); r = abs(w); r1=r/(Fs*t/2);
beep; wavplay(y*sh, Fs);
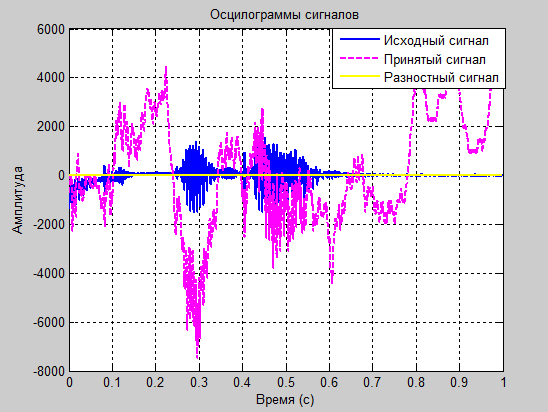
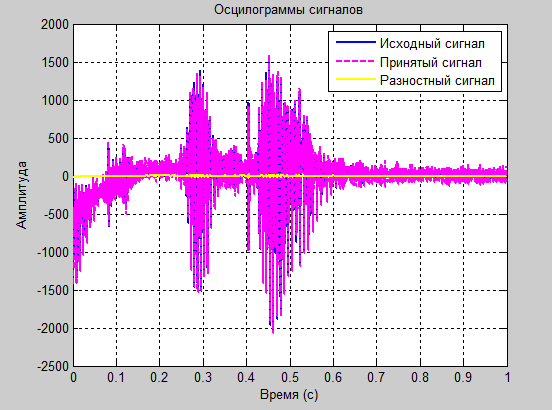
figure plot(tm,y,'--b',tm,x,':r',tm,e1,'y'); title('Синий - y, красный - x, желтый - разностный сжатый');% Подпись графика
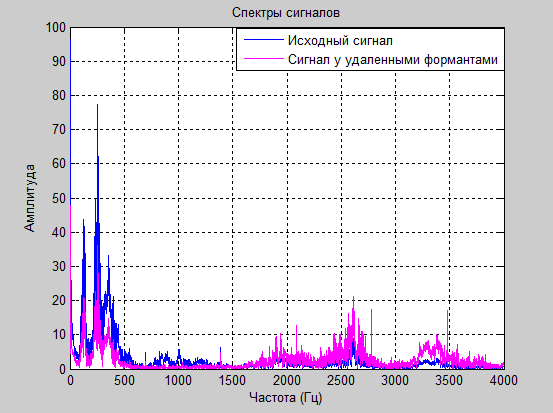
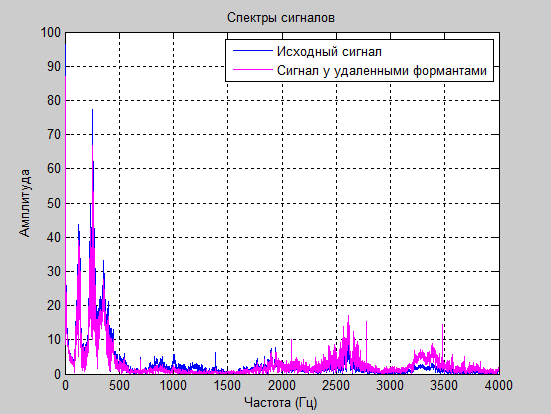
figure% Создаем новое окно plot(f,m1,'b',f,r1,'m') title('Спектры сигналов. Синий - исходный сигнал, сиреневый - с удаленными формантами');% Подпись графика xlabel('Частота (Гц)'), grid on;% Подпись оси х графика ylabel('Амплитуда'), grid on;% Подпись оси у графика
file_x=fopen('x_predicted.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', pr_x(n)); end fclose(file_x);
file_x=fopen('x.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', x(n)); end fclose(file_x);
file_x=fopen('e_before_commpression.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', e2(n)); end fclose(file_x);
file_x=fopen('e_commpressed.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', e1(n)); end fclose(file_x);
file_x=fopen('e_reconstructed.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', e(n)); end fclose(file_x);
file_x=fopen('y_predicted.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', pr_y(n)); end fclose(file_x);
file_x=fopen('y.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', y(n)); end fclose(file_x);
При помощи вышеописанной программы получим осциллограммы и спектрограммы речевого сигнала при произношении фразы «sixty two» и определим какие коэффициенты будут оптимальными в этом случае. Эксперимент № 1
а1=1.8 и а2=-0.8
Рис. 18
Рис. 19
Эксперимент № 2
а1=1.8 и а2=-0.9
Рис. 20
Рис. 21
Эксперимент № 3
а1=1.4 и а2=-0.9
Рис. 22
Рис. 23
Эксперимент № 4
а1=1 и а2=-0.9
Рис. 24
Рис. 25
Эксперимент № 5
а1=1.8 и а2=-1
Рис. 26
Рис. 27
Проанализировав полученные результаты: таблицы значений, осциллограммы и спектрограммы сигналов следует сделать вывод о том, что оптимальными для передачи речевого сигнала являются коэффициенты а1=1.8 и а2=-0.9. Именно при этих значениях можно соблюсти баланс между заметным уменьшением разностного сигнала и качеством восстановленного сигнала.
|

 8000 Гц и квантуем полученные отсчеты 2048 уровнями (11 бит и 1 бит на знак). Получим разностный сигнал также, как и в случае для синусоидального сигнала.
8000 Гц и квантуем полученные отсчеты 2048 уровнями (11 бит и 1 бит на знак). Получим разностный сигнал также, как и в случае для синусоидального сигнала.