Постановка задачи. Сжатие синусоидального сигнала с помощью ДИКМ.
В ходе выполнения данной лабораторной работы необходимо промоделировать ситуации сжатия сигнала методами в 2-х случаях: сигнал представлен синусоидальным колебанием и непосредственно речевым сигналом. При этом следует определить, какие коэффициенты линейного предсказания являются оптимальными. Пусть имеется исходный сигнал, изменяющийся по закону
где A = 0.5 и
Возьмем отсчеты этой синусоиды с частотой дискретизации
Определим значения предсказанных отсчетов как
Тогда разностный сигнал (сигнал ошибки), будет равен:
Благодаря выбору оптимальных коэффициентов a1 и a2 считаем, что полученные отсчеты разностного сигнала будут обладать разрядностью в два раза меньшей, чем отсчеты исходного. То есть значение разностного сигнала должно лежать в пределах от -31 до 31.Если же значение разностного сигнала превышает по модулю границы этих пределов, то в канал отправляем значение -31 или 31,в зависимости от знака е1. Следовательно, разностный сигнал e2(n), передаваемый в канал, можно записать согласно (2.4):
Тогда на приемной стороне по значением предсказанного сигнала (2.5) и разностного сигнала e2(n) получаем значение восстановленного сигнала(2.6):
Вышеописанный алгоритм реализуем при помощи технологии Matlab. Ниже приведен подробный листинг программы:
clear all; a1=1.8; a2=-0.8; t=0.2; Fs=8000; A=1; F=10; Phi=0; tm=0:1/Fs:t; x=A*sind((F*360).*tm+Phi); [x1,sh,kvbin,x]=DAC(x,Fs,t,12,2); q = fft(x,Fs*t); q = q(1:(Fs*t/2)); m = abs(q); m1=m/(Fs*t/2); f = (0:((Fs*t)-1)/2)/t; tm=tm(1:Fs*t); x=x(1:Fs*t);
for n=1:Fs*t if n==1 pr_x(n)=0; elseif n==2 pr_x(n)=round((a1*x(n-1))); else pr_x(n)=round(((a1*x(n-1)+a2*x(n-2)))); end
end for n=1:Fs*t if n==1 e(n)=x(n); else e(n)=x(n)-pr_x(n); end
end st=6;
for n=1:Fs*t if e(n)>0 if e(n)>(2^(st-1))-1 e(n)=(2^(st-1))-1; end elseif e(n)<0 if e(n)<-((2^(st-1))-1) e(n)=-((2^(st-1))-1); end end end
diff=e; diff_pr=e; for n=1:Fs*t if n==1 y(n)=e(n); pr_y(n)=0; elseif n==2 pr_y(n)=round((a1*y(n-1))); y(n)=e(n)+pr_y(n); else pr_y(n)=round(((a1*y(n-1)+a2*y(n-2)))); y(n)=e(n)+pr_y(n); end diff(n)=((y(n)-x(n))^2)^0.5; diff_pr(n)=pr_x(n)-pr_y(n);
end dif_sr=0; for i=1:Fs*t
dif_sr=dif_sr+diff_pr(n); end dif_sr=dif_sr/Fs*t; error1=e; error1(1)=0; error=0; e1(1)=e(1); e1(2)=e(2); for n=1:Fs*t
error=error+((x(n)-y(n))^2); if n==1 error1(n)=((x(n)-y(n))^2); else error1(n)=error1(n-1)+((x(n)-y(n))^2); end end %figure %plot(tm,error1); w = fft(e,Fs*t); w = w(1:(Fs*t/2)); r = abs(w); r1=r/(Fs*t/2); f=f(1:20); r1=r1(1:20); m1=m1(1:20);
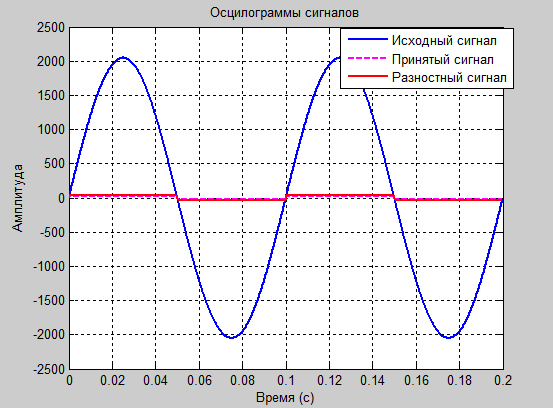
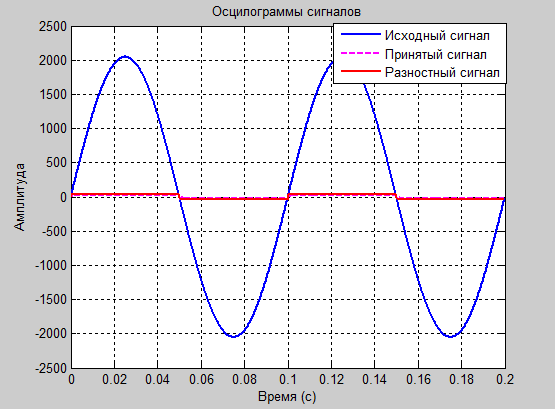
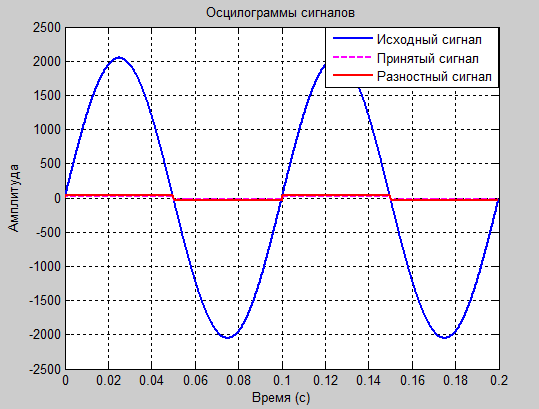
figure plot (tm,y); plot(tm,x,'b',tm,y,'--m',tm,e,'r','LineWidth',1.5) title('Осцилограмма сигнала');% Подпись графика xlabel('Время (с)'), grid on;% Подпись оси х графика ylabel('Амплитуда'), grid on;% Подпись оси у графика %figure %plot(tm,pr_x,'b',tm,pr_y,'--m','LineWidth',1.5) %title('Осцилограмма ПРЕДСКАЗАННОГО сигнала');% Подпись графика %xlabel('Время (с)'), grid on;% Подпись оси х графика %ylabel('Амплитуда'), grid on;% Подпись оси у графика
%figure %plot(tm,diff_pr,'b','LineWidth',1.5) %title('Осциллограмма разности предсказаний сигнала');% Подпись графика %xlabel('Время (с)'), grid on;% Подпись оси х графика %ylabel('Амплитуда'), grid on;% Подпись оси у графика
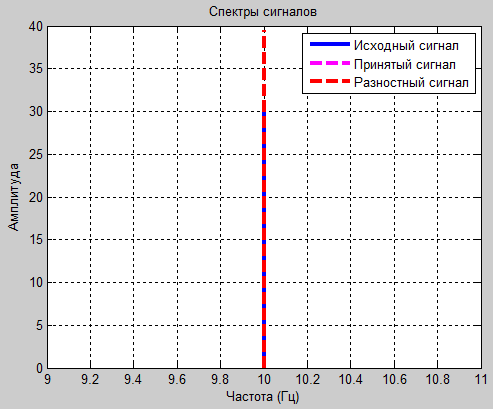
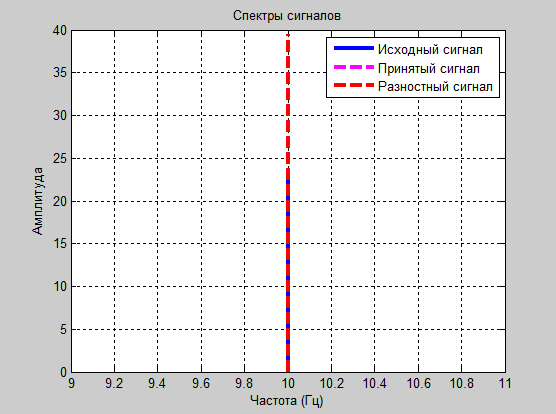
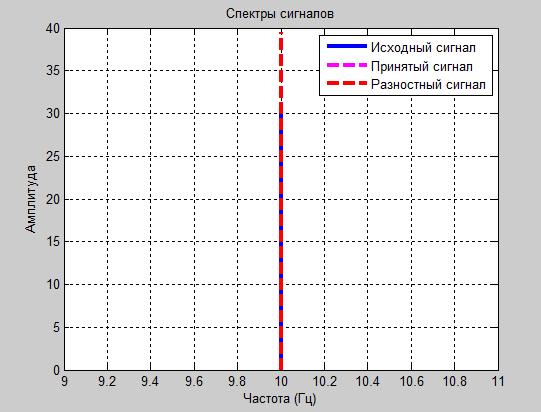
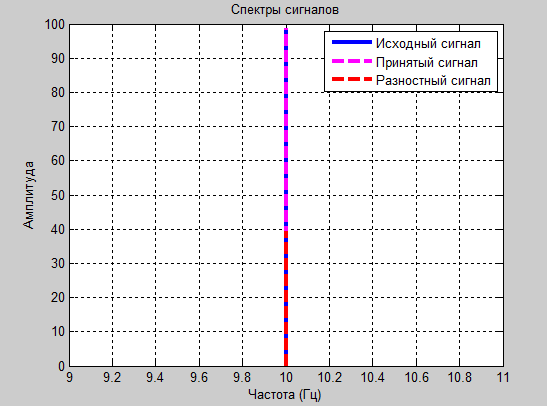
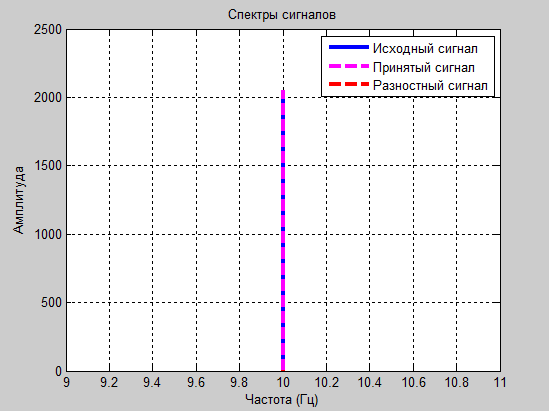
figure% Создаем новое окно plot(f,m1,'r',f,r1,'b','LineWidth',1.5); title('Спектр сигнала, красным спектр исходного сигнала, синим - разностного');% Подпись графика xlabel('Частота (Гц)'), grid on;% Подпись оси х графика ylabel('Амплитуда'), grid on;% Подпись оси у графика
%figure %plot(tm,diff,'b','LineWidth',1.5);
%title('Осциллограмма разности сигналов');% Подпись графика %xlabel('Время (с)'), grid on;% Подпись оси х графика
file_x=fopen('x_sinus.txt','wt'); for n=1:Fs*t; fprintf(file_x,'%f\n', x(n)); end fclose(file_x);
file_x=fopen('pr_x_sinus.txt','wt'); for n=1:Fs*t; fprintf(file_x,'%f\n', pr_x(n)); end fclose(file_x);
file_x=fopen('pr_y_sinus.txt','wt'); for n=1:Fs*t; fprintf(file_x,'%f\n', pr_y(n)); end fclose(file_x); % % % file_x=fopen('e_sinus.txt','wt'); for n=1:Fs*t;%
fprintf(file_x,'%f\n', e(n)); end fclose(file_x);
file_x=fopen('y_sinus.txt','wt'); for n=1:Fs*t; fprintf(file_x,'%f\n', y(n)); end fclose(file_x);
Введенная подпрограмма “DAC” – подпрограмма квантователя. Ее листинг проиллюстрирован ниже:
function [kvant,sh,kvbin, kv]=DAC(x,Fs,t,n,sh) %АЦП if sh==2 xx=abs(x); sh=max(xx)/2^(n-1); else xx=abs(x); sh=sh; end for s0=1:Fs*t i=2^(n-1)-1;
if x(s0)<0 for s1=1:2^(n-1) if xx(s0)<i*sh i=i-1; else if xx(s0)>(i+1)*sh-sh/2 kv(s0)=(i+1)*-1; else kv(s0)=i*-1;
end end end elseif x(s0)>0 for s1=1:2^(n-1) if xx(s0)<i*sh i=i-1; else if xx(s0)>(i+1)*sh-sh/2 kv(s0)=(i+1); %kvb(s0)=de2bi(i+1); else kv(s0)=i; %kvb(s0)=de2bi(i);
end end end elseif x(s0)==max(s0) kv=i;
else kv(s0)=0;
end
end kvb=de2bi(abs(kv)); kvb1=zeros(Fs*t,n);
%for s3=1:Fs*t % if x(s3)<0 % zn=0; % % else % zn=1; % end % kvb1(s3,1)=de2bi(zn); % lo=kvb(s3,:); % kvb1(s3,2:n)= lo; %end kvant=kv*sh; kvbin=kvb1;
end
Воспользовавшись вышеприведенной программой, будем изменять коэффициенты а1 и а2 таким образом, чтобы подобрать оптимальные коэффициенты для передачи синусоидального сигнала. Представим полученные при этом спектрограммы и осциллограммы сигнала для различных пар коэффициентов а1 и а2. Временные диаграммы отсчетов исходного сигнала (x), предсказанного на передающей стороне (
Эксперимент № 1
а1=0.1 и а2=-0.4
Рис. 2
Рис. 3
Эксперимент № 2
а1=0.1 и а2=-0.8
Рис. 4
Рис. 5
Эксперимент № 3
а1=0.5 и а2=-0.8
Рис. 6
Рис. 7
Эксперимент № 4
а1=1.4 и а2=-0.8
Рис. 8
Рис. 9
Эксперимент № 5
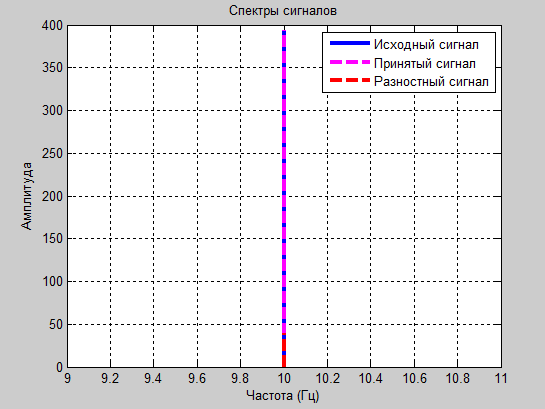
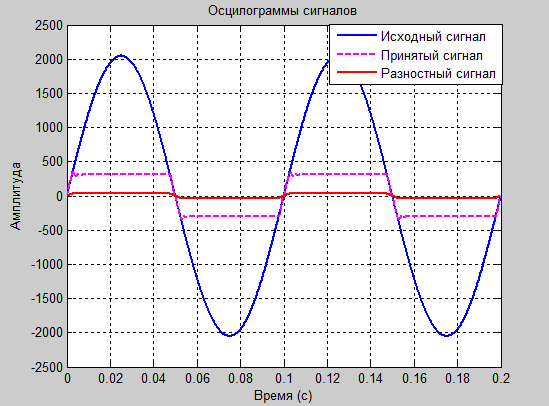
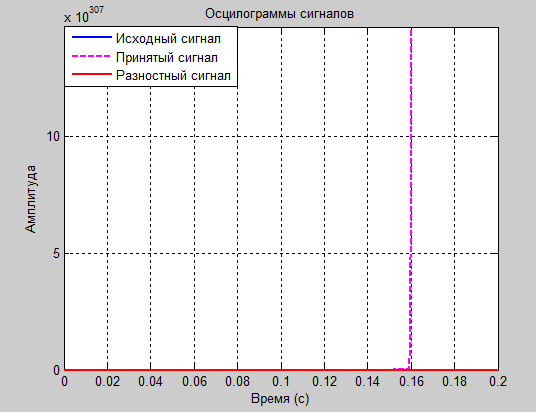
а1=1.8 и а2=-0.8
Рис. 10
Рис. 11
Эксперимент № 6
а1=1.8 и а2=-0.9
Рис. 12
Рис. 13
Эксперимент № 7
а1=1.8 и а2=-1.2
Рис. 14
Рис. 15
Эксперимент № 8
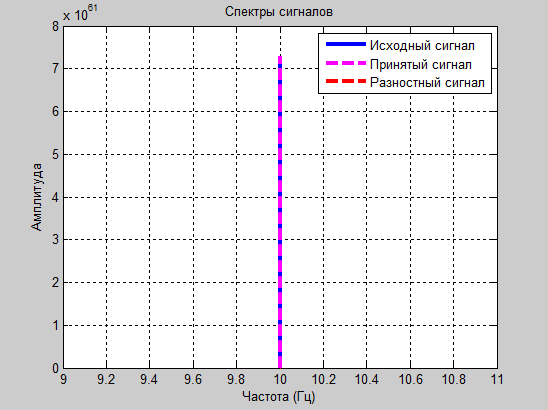
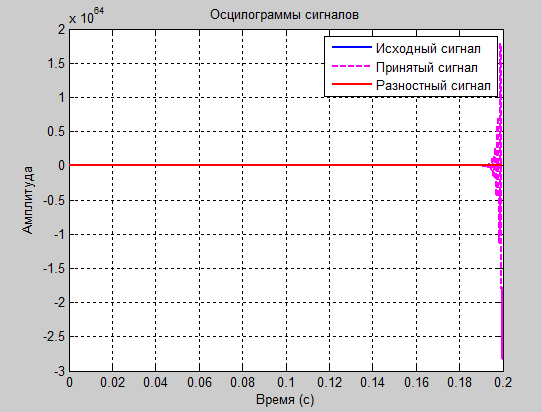
а1=2.2 и а2=-0.8
Рис. 16
Рис. 17
Проанализировав полученные результаты: таблицы значений, осциллограммы и спектрограммы сигналов, следует сделать вывод о том, что оптимальными для передачи синусоидального сигнала являются коэффициенты а1=1.8 и а2= -0.8. Именно при этих значениях зможно передать разностный сигнал в пределах 6 бит и получить итоговый сигнал без заметных искажений.
|

 (2.1)
(2.1)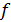 =10 Гц
=10 Гц 8000 Гц и квантуем полученные отсчеты 2048 уровнями (11 бит и 1 бит на знак). Получим последовательность входных отсчетов x(n), значения которых будем представлять в соответствующих уровнях квантования.
8000 Гц и квантуем полученные отсчеты 2048 уровнями (11 бит и 1 бит на знак). Получим последовательность входных отсчетов x(n), значения которых будем представлять в соответствующих уровнях квантования. (2.2)
(2.2) (2.3)
(2.3)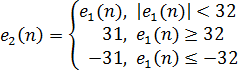 (2.4)
(2.4) (2.5)
(2.5)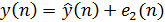 (2.6)
(2.6) ), разностного (e), предсказанного на приемной стороне(
), разностного (e), предсказанного на приемной стороне( ) и принятого сигнала (y), и спектрограммы этих сигналов, представлены ниже.
) и принятого сигнала (y), и спектрограммы этих сигналов, представлены ниже.