Общая идея заключается в предварительной «аппроксимации» уравнения и последующем точном решении «аппроксимирующего» уравнения. Аппроксимирующее уравнение конструируется так, что его решение сводится к рассмотрению конечной системы скалярных уравнений.
Пусть E и F – банаховы пространства (комплексные или вещественные). Рассмотрим уравнение
 , (1)
, (1)
где L – линейный (вообще говоря, неограниченный) оператор с областью определения  и областью значений
и областью значений  . Проекционный метод решения этого уравнения заключается в следующем. Задаются две последовательности подпространств
. Проекционный метод решения этого уравнения заключается в следующем. Задаются две последовательности подпространств 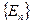 и
и  ;
;

а также линейные проекционные операторы (проекторы)  , проектирующие F на
, проектирующие F на 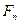 , т.е. операторы, удовлетворяющие условиям
, т.е. операторы, удовлетворяющие условиям

Уравнение (1) заменяется приближенным
 (2)
(2)
решение ищется в 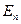 .
.
В случае 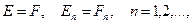 проекционный метод (2) называют методом Галеркина.
проекционный метод (2) называют методом Галеркина.
Пусть пространства E и F гильбертовы. Задаются две полные последовательности  и
и 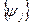 ,
,
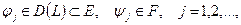
(это так называемые координатные последовательности). Приближенное решение ищется в виде линейной комбинации
 (3)
(3)
и определяется из условия ортогональности невязки 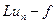 первым n элементам второй координатной последовательности:
первым n элементам второй координатной последовательности:

Это приводит к линейной системе уравнений для отыскания коэффициентов 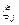 :
:
 (3’)
(3’)
Видно, что условия (3), (3’) равносильны условиям (2), в которых 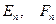 - линейные оболочки элементов
- линейные оболочки элементов  и
и  соответственно, а
соответственно, а  - оператор ортогонального проектирования на подпространство
- оператор ортогонального проектирования на подпространство 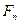 (ортопроектор). Ортогональность проектирования
(ортопроектор). Ортогональность проектирования  и является наиболее существенным требованием. Описанный метод называют методом Галеркина – Петрова. В методе Галеркина – Петрова подпространства
и является наиболее существенным требованием. Описанный метод называют методом Галеркина – Петрова. В методе Галеркина – Петрова подпространства 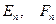 конечномерны и
конечномерны и

Иногда под методом Галеркина – Петрова понимают проекционный метод (2) с ортопроекторами  и в том случае, когда соответствующие подпространства бесконечномерны и когда нет указанных вложений.
и в том случае, когда соответствующие подпространства бесконечномерны и когда нет указанных вложений.
При приближенном решении методом Галеркина – Петрова конкретных уравнений координатные последовательности  и
и 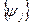 можно выбирать различными способами. Например, часто элементы
можно выбирать различными способами. Например, часто элементы  выбирают по элементам
выбирают по элементам  при помощи равенств
при помощи равенств

В этом случае говорят о методе наименьших квадратов.
Если гильбертовы пространства E и F совпадают и если обе координатные последовательности одинаковы  , то метод Галеркина – Петрова принято называть методом Бубнова – Галеркина.
, то метод Галеркина – Петрова принято называть методом Бубнова – Галеркина.
Рассмотрим уравнение
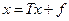 , (4)
, (4)
где T – линейный непрерывный оператор в банаховом пространстве E. Пусть 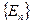 - последовательность замкнутых подпространств E. В качестве приближенных решений уравнения (4) принимаются решения уравнений
- последовательность замкнутых подпространств E. В качестве приближенных решений уравнения (4) принимаются решения уравнений
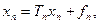 (5)
(5)
где  - линейный непрерывный оператор в
- линейный непрерывный оператор в 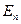 ,
,  .
.
Характеристикой близости уравнений (4) и (5) не может служить разность операторов T и  , т.к. эти операторы действуют в различных пространствах. Пусть
, т.к. эти операторы действуют в различных пространствах. Пусть  - проектор (вообще говоря, неограниченный), проектирующий в подпространство
- проектор (вообще говоря, неограниченный), проектирующий в подпространство 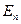 :
:
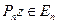 для
для  ,
, 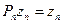 для
для  .
.
Пусть 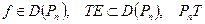 - ограниченный в E (а значит, и в
- ограниченный в E (а значит, и в 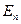 ) оператор. Каждый из операторов T и
) оператор. Каждый из операторов T и  можно сравнивать с
можно сравнивать с 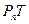 , рассматривая его соответственно как оператор в E или в
, рассматривая его соответственно как оператор в E или в 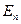 . Т.о. характеристиками близости уравнений (4) и (5) естественно брать норму оператора
. Т.о. характеристиками близости уравнений (4) и (5) естественно брать норму оператора  в
в 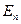 и норму оператора
и норму оператора 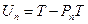 в E, а также нормы
в E, а также нормы 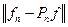 и
и  . Другими словами, каждое из уравнений (4) и (5) сравнивается с галеркинским уравнением
. Другими словами, каждое из уравнений (4) и (5) сравнивается с галеркинским уравнением
 (6)
(6)
Последнее уравнение, в отличие от уравнений (4) и (5), может рассматриваться как в пространстве E, так и в подпространстве 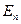 .
.
Уравнение (5) иногда удобнее записывать в форме
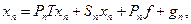 (7)
(7)
где  и
и  характеризуют отклонение уравнения (5) от галеркинского уравнения (6). Рассматриваются случаи, когда эти отклонения малы (
характеризуют отклонение уравнения (5) от галеркинского уравнения (6). Рассматриваются случаи, когда эти отклонения малы ( ). Соответствующие приближенные методы объединяют под названием метод Галеркина с возмущениями (например, метод механических квадратур).
). Соответствующие приближенные методы объединяют под названием метод Галеркина с возмущениями (например, метод механических квадратур).

 , (1)
, (1) и областью значений
и областью значений  . Проекционный метод решения этого уравнения заключается в следующем. Задаются две последовательности подпространств
. Проекционный метод решения этого уравнения заключается в следующем. Задаются две последовательности подпространств 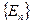 и
и  ;
;
 , проектирующие F на
, проектирующие F на 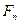 , т.е. операторы, удовлетворяющие условиям
, т.е. операторы, удовлетворяющие условиям
 (2)
(2)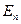 .
.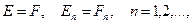 проекционный метод (2) называют методом Галеркина.
проекционный метод (2) называют методом Галеркина. и
и 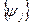 ,
,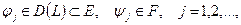
 (3)
(3)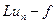 первым n элементам второй координатной последовательности:
первым n элементам второй координатной последовательности:
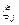 :
: (3’)
(3’)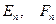 - линейные оболочки элементов
- линейные оболочки элементов  и
и  соответственно, а
соответственно, а 
 выбирают по элементам
выбирают по элементам  при помощи равенств
при помощи равенств
 , то метод Галеркина – Петрова принято называть методом Бубнова – Галеркина.
, то метод Галеркина – Петрова принято называть методом Бубнова – Галеркина.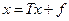 , (4)
, (4)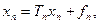 (5)
(5) - линейный непрерывный оператор в
- линейный непрерывный оператор в  .
.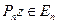 для
для  ,
, 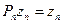 для
для  .
.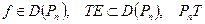 - ограниченный в E (а значит, и в
- ограниченный в E (а значит, и в 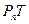 , рассматривая его соответственно как оператор в E или в
, рассматривая его соответственно как оператор в E или в  в
в 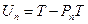 в E, а также нормы
в E, а также нормы 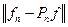 и
и  . Другими словами, каждое из уравнений (4) и (5) сравнивается с галеркинским уравнением
. Другими словами, каждое из уравнений (4) и (5) сравнивается с галеркинским уравнением (6)
(6)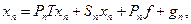 (7)
(7) и
и  характеризуют отклонение уравнения (5) от галеркинского уравнения (6). Рассматриваются случаи, когда эти отклонения малы (
характеризуют отклонение уравнения (5) от галеркинского уравнения (6). Рассматриваются случаи, когда эти отклонения малы ( ). Соответствующие приближенные методы объединяют под названием метод Галеркина с возмущениями (например, метод механических квадратур).
). Соответствующие приближенные методы объединяют под названием метод Галеркина с возмущениями (например, метод механических квадратур).


