Нормальное распределение. Непрерывной СВ Х называется распределенной по нормальному закону, если ее плотность вероятности имеет вид: р(х)= 1/ *
Непрерывной СВ Х называется распределенной по нормальному закону, если ее плотность вероятности имеет вид: р(х)= 1/ 56. Выборкой объема n из генеральной совокупности называется значения x1,x2,…,xn наблюдаемой СВ Х отвечающие независимым повторениям эксперимента. Совокупность значений x1,x2,…,xn расположенных по не убыванию называются вариационным рядом. Статистический ряд – это совокупность пар (xi,ni) где xi – разные элементы выборки ni - частота появления xi в выборке:
Числовые характеристики М(х) = а, Д(х)=σ2, Р(⍺˂х˂β)=Ф(β-а/σ) – Ф(⍺-а/σ) Р( F(x)=1/
1. Определенный интеграл как предел интегральных сумм, условия интегрируемости. 2. Основные свойства, оценки определенного интеграла. 3. Теорема о среднем. Среднее значение функции на отрезке. 4. Производная определенного интеграла по переменному верхнему пределу. 5. Формула Ньютона-Лейбница. 6. Замена переменной, интегрирование по частям в опр. интеграле. Интегр-е по промежутку [-a,a] чет. и нечет. функции. 7. Вычисление площади криволинейного сектора в полярных координатах. 8. Вычисление длины дуги в декартовых, полярных координатах, кривой, заданной параметрически. 9. Вычисление объема тела вращения. 10. Вычисление работы переменной силы. 11. Несобственные интегралы с бесконечными пределами интегрирования. 12. Несобственные интегралы от неограниченных функций. 13. Понятия диф. уравнения, общего и частного решений.Теорема существования и единственности решения задачи Коши. 14. Дифференциальные уравнения первого порядка с разделяющимися переменными. 15. Однородные дифференциальные уравнения первого порядка, метод их решения. 16. Линейные дифференциальные уравнения I-го порядка: общий вид, метод решения. Уравнение Бернулли. 17. Дифференциальные уравнения второго порядка, допускающие понижение порядка. 18. Линейные однородные дифференциальные уравнения 2-го порядка, теорема о структуре общего решения. 19. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. 20. Теорема о структуре общего решения линейного неоднородного диф. уравнения. 21. Метод вариации произвольных постоянных. 22. Метод неопределенных коэффициентов для решения ЛНДУ со специальной правой частью. Теорема о наложении решений ЛНДУ. 23. Двойной интеграл, его свойства, геометрические и физические приложения. 24. Тройной интеграл, его свойства, применение к вычислению объемов. 25. Криволинейный интеграл 1-го рода (по длине дуги), его свойства, приложения. 26. Криволинейный интеграл 2-го рода (по координатам), его свойства, приложения. 27. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования. Формула Грина. 28. Поверхностные интегралы I рода. 29. Поверхностные интегралы II рода. 30. Определение векторного поля. Поток, циркуляция. 31. Ротор, дивергенция. Потенциальное и соленоидальное вект.поля. 32. Понятие ряда, сходящегося и расходящегося ряда. Осн. свойства числовых рядов. Необходимый признак сходимости. 33. Достаточные признаки сходимости рядов с положительными членами (признаки сравнения, признак Даламбера). 34. Интегральный признак сходимости числовых рядов с положительными членами. Обобщенный гармонический ряд. 35. Признак Лейбница сходимости знакочередующегося ряда. 36. Абсолютная и условная сходимость знакопеременного ряда. 37. Степенные ряды. Теорема Абеля. Радиус, интервал, область сходимости. 38. Ряд Тейлора (Маклорена). Разложение функции в степенной ряд. Единственность разложения. 39. Ряды Маклорена для функций 40. Приложения степенных рядов к вычислению значений функций, определенных интегралов, решений диф. уравнений. 41. Пространство элементарных исходов. Сумма, произведение событий. 42. Классическое определение вероятности случайного события. Геометрическая вероятность. 43. Теоремы сложения вероятностей для несовместных и совместных событий. 44. Условная вероятность. Теоремы умножения вероятностей для зависимых и независимых событий. 45. Формула полной вероятности. Формула Байеса. 46. Схема Бернулли. Формулы Бернулли, Пуассона. Теоремы Лапласа. 47. Понятие случайной величины. Функция распределения и ее свойства. 48. Дискретные случайные величины, их числовые характеристики. 49. Биномиальное распределение и его числовые характеристики. Распределение Пуассона, его числовые характеристики. 50. Непрерывные случайные величины. Плотность вероятностей, ее свойства. Числовые характеристики непрерывной СВ. 51. Равномерное распределение случайной величины и его числовые характеристики. 52. Показательное распределение. 53. Нормальный закон распределения случайной величины. 54. Понятие о системах случайных величин. Функция распределения, плотность распределения. Числовые характеристики. 55. Теорема Бернулли. Теорема Ляпунова. 56. Выборка, вариационные и статистические ряды и их графическое изображение. Эмпирическая функция распределения. 57. Оценки параметров распределения. Точечное и интервальное оценивание.
|

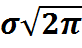 *
* 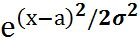
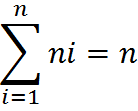
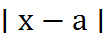 ˂
˂ 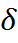 )= 2Ф
)= 2Ф 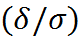
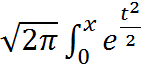 dt
dt


