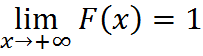Теорема: пусть функция u(x), v(x) и их производные u,(x), v,(x), непрерывны на [a,b], тогда справедлива формула .
Метод замены переменных в определенном интеграле: Теорема: пусть функция f(x) непрерывна на [a,b], а функция x=ϕ(t) непрерывно-дифференцируема на [α,β], причем ϕ(α)=а, ϕ(β)=b и функция a≤ϕ(t)≤b, тогда имеет место формула:
Интегрирование четных и нечетных функций:пусть функция f(x)непрерывна на [a,b], тогда вычисление интеграла
7. Вычисление площади в декартовой системе координат:
f2(x)
f2≥f1 S=
Параметрическое задание: x(α)=a, x(β)=b В полярных координатах:
12. Несобственные интегралы второго рода: Пусть f(x) непрерывна на промежутке [a,b) и неограниченна при x→b (f(x)→∞ при x→b) в этом случае несобственный интеграл 2-го рода принимают следующим образом: Если предел существует, говорят, что интеграл сходится, не существует или бесконечен – расходится. Теорема (сравнения):пусть на промежутке [a,b) функции f(x), ϕ(x) непрерывны и f(x)→∞, ϕ(x)→∞ при x→b при этом 0≤f(x)≤ϕ(x) тогда из сходимости интеграла: Теорема (предельный признак сравнения): пусть на промежутке [a,b) функции f(x), ϕ(x) непрерывны и f(x)→∞, ϕ(x)→∞ при x→b при этом 0≤f(x)≤ϕ(x) если существует предел: 9. Вычисление объема тела вращения: Пусть вокруг оси Ох вращения криволинейная трапеция, ограниченная кривой у=f(x), прямыми х=0, х=в и Ох и пусть f(x) непрерывная на [a,b] функции (f˃0), получим тело вращения V которого вычисляется по формуле: (Vox=π; Разобьем отрезок [a,b] на n частей в каждой части произвольно выберем точку Ci ϵ [Xi-1,X1], проведем, через точки Xi плоскости ˔ Ох получим слоев тела вращения, каждый слой замещением цилиндра высотой ΔXi=Xi-Xi-1 и основанием является круг радиуса f(Ci). Сумарный объем ступенчатого тела равен
10. Работа переменной силы: Пусть материальная точка переменной под действием силы F направленной вдоль оси Ох и имеющей переменную величину зависящей от х F=F(x), покажем, что работа совершаемая силой F по перемещению точки вдоль оси Ох из х=а в х=в вычисляется по формуле: A= (F, непрерывна на [a,b])
11. Несобственные интеграла с бесконечными пределами интегрирования: Пусть функция f(x) непрерывна на [a,+∞], тогда по определению полагают: Если существует конечные предел в * то говорят, что Н.И. сходится, если предел не существует или бесконечен – интеграл называется расходящимся. Для исследования сходимости:
Предельный признак сходимости:если существует предел Теорема 3: из сходимости интеграла
13. Уравнение связывающее независимую переменную, искомую функцию и ее производные называется дифференциальным уравнением (ДУ). Решением ДУ называется функция которая при подстановке в уравнение обращают его в тождество. Общим решением ДУ первого порядка называется функция у=ϕ(х,с), содержащее одну произвольную постоянную и удовлетворяющая следующим условиям: 1). Она является решением ДУ при каждом фиксируемом значении С. 2). Каково бы ни было начальное условие y(x0)=y0 найдется такое значение произвольной постоянной с=С0, что функция у=ϕ(х,с0) будет удовлетворять заданному начальному условию. Частным решение ДУ первого порядка называют любую функцию у=ϕ(х,с0) полученную из ОР при конкретных значениях постоянной. Теорема:Если функция f(x,y) м ее частная производная f’(x,y) непрерывны в некоторой области Д содержащей точку(х0,у0), то существует единственное решение у=у(х) ДУ y’=f(x,y) удовлетворяющее начальному условию.
17. 1-ый тип: уравнения не содержащие явно искомую функцию у: F(x,y’,y’’)=0. Уравнение допускает понижение порядка(т.е. сводится к уравнению более низкого порядка – к первому) с помощью замены y’=z(x), где z(x)-новая неизвестная функция, тогда y’’=z’ и уравнение примет вид F(x,z,z’),решая его находим функцию z(x)=ϕ(x,C1), в итоге искомая функция у находится интегрированием:
2-ой тип: уравнение не содержащее явно независимую переменную х: F(y,y’,y’’)=0. Примени метод понижения порядка, сделаем замену: y’=p(y) y’’=(p(y))’x=dp/dy*y’x=pdp/dy,уравнение примет вид F(y,p,pdp/dy)=0 - ДУ 1-го порядка, откуда находим функцию p=ϕ(y,C1) или dy/dx=ϕ(y,C1)–с разделяющими переменными (РАЗДЕЛИТЬ ПЕРЕМЕННЫЕ). Du/ϕ(y,C1)=dx. Далее интегрируем.
18. ЛОДУ 2-го порядка: y’’+p(x)y’+q(x)y=0 * Функции y1(х),y2(х) называются линейно-зависимыми на (а,в), если существуют такие числа α1,α2, из которых хотя бы одно отлично от 0, что выполняется равенство α1y1(х)+α2y2(х)=0 для любых х из интервала (а,в). Если же из выполнения указанного равенства следует, что α1=α2=0, то функции y1(х),y2(х) называются линейно-независимыми на (а,в). О линейно-зависимых или независимых y1(х),y2(х) можно судить по определителю:
Теорема: (о структуре ОР ЛОДУ 2-го порядка) если y1(х) и y2(х) линейно-независимые решения уравнения (*), то функция y=C1*y1(x)+C2*y2(x)-где С1,С2 – произвольные постоянные являющиеся общим решением уравнения (*).
19. ЛОДУ 2-го порядка с постоянными коэффициентами: y’’+py’+qy=0 1. Д˃0 к1≠к2 к1,к2=(-p+(-) 2. Д=0 к1=к2=к к=-p/2 (y1=ekx y2=ekxx) OP (y=C1ekx+C2ekxx) 3. Д˂0 Д=-р-4q˂0 k1,k2=(-p+(-)i OP (y=C1eαxcos(βx)+C2eαxsin(βx)=eαx(C1cos(βx)+C2sin(βx))
20. ЛНДУ 2-го порядка: y’’+py’+qy=f(x) Теорема(о структуре ОР ЛНДУ 2-го порядка) общим решением ЛНДУ является сумма общего решения однородного уравнения соответствующее y’’+py’+qy=f(x) и некоторого частичного решения уравнения y’’+py’+qy=f(x): yон=уоо+учн
21. Метод вариации произвольных постоянных: Пусть y=C1(x)y1+C2(x)y2-где С1(х),С2(х) некоторые функции подлежащие определению Для нахождения С1(х),С2(х) потребуем чтобы учн было решением уравнения y’’+py’+qy=f(x) (*) Найдем учн’ = C1(х)’y1++C1(x)y1’+C2(x)’y2+C2(x)y2’, пусть для упрощения C1’(x)y1+C2’(x)y2=0, тогда y’чн=C1(x)y1’+C2(x)y2’, далее y’’чн=C1’(x)y1’+C1(x)y1’’+C2’(x)y2’+C2(x)y2’’ подставляем в уравнение (*). Требуем (…………..)=f(x), и так, чтобы y=C1(x)y1+C2(x)y2 было решением уравнения, должны выполнятся следующие требования: Из полученной системы определяем С1’(х), С2’(х), находим С1(х), С2(х): интегрированием
Записываем учн=С1(х)у1+С2(х)у2, после чего уон=уоо+учн
22. Метод неопределенных коэффициентов(метод подбора)
23. Если существует предел интегральной суммы Свойства двойного интеграла: 1.Линейность: 2. Аддитивность: 3. Монотонность: а). если f(x,y)≥0 в Д, то 4. Оценка двойного интеграла: пусть м- наименьшее, М- наибольшее значения функции z=f(x,y) в области Д, тогда m(Sd)≤ 5. Аналог теоремы о среднем: пусть f(x,y) непрерывна в Д, тогда существует М0(х0,у0) ϵ Д что S(x)= V=
24. Если существует предел интегральной суммы Свойства тройного интеграла: 1. Линейность 2. Аддитивность: 3. Монотонность: если f(x,y,z)≤g(x,y,z) 4. 5. 6. 7. p=p(x,y,z)
25. Если существует предел интегральной суммы Свойства КРИ-1: 1. 2. 3. 4. f(x,y)≤g(x,y), 5. 6. p(x,y), m= 7.
27. пусть функция Р(х,у), Q(х,у) непрерывны вместе со своими частными производными в области Д, тогда имеет место формула:
-где Условия независимости КРИ-2: 1. Для любой замкнутой кривой 2. Для любых 2-х точек А и В лежащих в Д значений интеграла 3. P(x,y)dx+Q(x,y)dy – представляет собой полный дифференциал некоторой функции u(x,y) определенного в области Д т.е. такой, что du=Pdx+Qdy 4. В области Д всюду: 28. Пусть задана поверхность S и функция f(x,y,z), разбивающая поверхность на части площадями Свойства: 1. f=1 2. Если задана плотность поверхности
29. Рассмотрим 3 непрерывные функции P(x,y,z), Q(x,y,z), R(x,y,z) и выберем определенную сторону поверхности S (ориентированную поверхность). Выбранную сторону S разбиваем на части, затем проектируем эти части на координатные плоскости и строим интегральные суммы например: Общий вид ПОВИ-2:
30. Если в каждой точке М некоторой области задан вектор Характеристики векторного поля: 1. Поток ПS(
2. Циркуляцией векторного поля вдоль замкнутой ориентированной кривой L, называется следующее КРИ-2: ЦL( 31. Дивергенцией векторного поля называется величина: Ротором (вихрем) векторного поля называется Если Векторное поле в каждой точке которого дивергенция равна 0, называется соленоидальным. 33. Достаточные признаки сравнения: 1. Признак сравнения: пусть даны 2 знака положительных ряда 2. Предельный признак сравнения:пусть даны 2 знака положительных ряда 3. Признак Даламбера: пусть дан знака положительный ряд При l˂1 ряд сходится При l˃1 ряд расходится При l=1 признак ответа не дает
34. Интегральный признак Коши: если члены знака положительного ряда могут быть представлены, как числовые значения некоторой непрерывной, монотонно убывающей на промежутке [1,∞) функции f(x), так что U1=f(1), U2=f(2) и т.д., а Un=f(n). 1. если 2. Если
38. Рядом Тейлора для функции f(x) называется ряд вида: Если модули всех производных функции f(x) ограничены в окрестности точки х0 одним и тем же числом М˃0, то для любых х из этой окрестности ряд Тейлора функции f(x) сходится к самой функции f(x), т.е. имеет место разложение: При х0=0 ряд Тейлора называется рядом Маклорена и имеет вид: 39. Ряды Маклорена для некоторых функций: 1). y=sinx (абсолютно сходится на всей числовой оси) 2). y=cosx (абсолютно сходится на всей числовой оси) 3). y= (абсолютно сходится на всей числовой оси) 4). y=ln(1+x)
(сходится, если х ϵ (-1,1]) 5). y=(1+x)m Если m целое, положительное число, то вместо ряда получается конечная сумма. Если m≥0 ряд сходится при хϵ [-1,1] -1˂m˂0, то xϵ(-1,1], m≤1, то xϵ(-1,1)
40. Приложения степенных рядов: · Приближенное вычисление Пусть требуется вычислить значение функции при х=х1 с заданной точностью ε функция раскладываем в степенной ряд подставляя вместо х, значения х1 и оставляем для вычисления столько членов ряда, сколько необходимо для соблюдения заданной точности ε. Для знака чередующихся рядов первый из отбрасываемых членов ряда должен быть по модулю меньше заданной точности. · Вычисление интегралов Отметим, что абсолютно сходящиеся ряды можно дифференцировать и интегрировать почленно, при этом также получаются сходящиеся ряды. Сперва разлаживаем под интегральную функцию в степенной ряд, затем интегрируем почленно. · Приближенное вычисление ДУ Запишем разложение в ряд Тейлора решение задачи Коши
43.Теорема(сложение вероятностей для несовместных событий):вероятность суммы 2-ч несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B) Теорема(сложения вероятностей для произвольных событий): вероятность суммы для произвольных событий равна сумме вероятностей этих событий без вероятности их произведения. P(A+B)=P(A)+P(B)-P(AB)
44. Вероятность события В, при условии, что произошло событие А, называется условной вероятностью события В и обозначается: P(B/A) Теорема: вероятность произведения двух событий А и В равна произведению вероятности одного из них, на условную вероятность другого в предположении, что первое имеет место: P (AB)=P(A)*P(B/A) Замечание: вероятность совместного появления 2-х независимых событий равна произведению вероятностей этих событий: P(AB)=P(A)*P(B)
45. Теорема: вероятность события А равна сумме произведений вероятностей всех гипотез на условную вероятность события А: Р(А)=P(H1)*P(A/H1)+..+P(Hn)P(A/Hn)=
Пусть имеется полная группа событий H1,H2,…,Hn вероятности которых P(H1),P(H2),…,P(Hn) известны до опыта(вероятности априори). Производится опыт (испытание) в результате которого зарегистрировано появление события А. Требуется найти вероятности гипотез после опыта (апостериори). т.е. фактически переоценить вероятности гипотез, т.к. P(AІHi)=P(A)*P(HiІA)=P(Hi)*P(AІHi) – откуда P(HiІA)=(P(Hi)*P(AІHi))/P(A)=(P(Hi)*P(AІHi))/∑P(Hi)*P(AІHi) – формула Байеса. 46. Серия повторений независимых испытаний в каждом из которых некоторое событие А происходило с одной и той же вероятностью р - называется схемой Бернулли. Т.о. в схеме Бернулли для каждого испытания возможны только 2 исхода: 1). Событие А происходит с вероятностью р. 2). Событие А не происходит с вероятностью 1-р=q.
Теорема(Пуассона):пусть вероятность появления события А в каждом из n–испытаний мала (близка к 0), а число испытаний достаточно велико, тогда вероятность того, что в испытаний событие Р наступит к- раз выражает формула Пуассона: Теоремы Лапласа: 1. пусть вероятность наступления события А в каждом n–независимых испытаний постоянно и равна p(0˂p˂1). Тогда вероятность того, что в –испытаний событие появится к- раз можно найти по приближенной формуле:
2. Интегральная: пусть вероятность того, что в –испытаний событие А произойдет не менее к1 и не более к2 раз определяется по формуле: Ф(-х)=-Ф(х)-нечетная, Ф(х)=1/2 для х˃5
49. ДСВ Х называется распределенной по биномиальному закону, если она принимает свои значения к с вероятностями вычисленными по формуле Бернулли: Характеристики:M(x)=np; D(x)=npq; σ= СВ Х называется распределенной по закону Пуассона, если вероятности с которыми она принимает свои значения вычисляется по формуле Пуассона: Характеристики:M(x)=np=λ; D(x)=np=λ; σ(x)=
50. Пусть функция распределения непрерывной СВ имеет производную F’(x)=p(x), тогда функция p(x) называется плотностью вероятности непрерывной случайной величины. Свойства плотности вероятности: 1. P(x)≥0 (P(x)) 2. 3. P(a˂x˂b)= 4. a=-∞ b=x p(-∞˂X˂x)=p(X˂x)=F(x) F(x)= Числовые характеристики непрерывной СВ: 1. под математическим ожиданием непрерывной СВ Х понимается величина несобственного интеграла:
2. D(X)= 3. σ(X)= 51. Непрерывной СВ Х называется равномерно распределенной, если ее плотность вероятности постоянна на отрезке [a,b], а вне этого отрезка =0, т.е. p(x)= Плотность вероятности распределения: F(x)= Числовые характеристики: 1. M(X)=(a+b)/2 2. D(X)=(b-a)2/12 3. Σ(X)=Іb-aІ/2
52. Распределение непрерывной СВ называется показательным, если плотность вероятности имеет вид: F(x)= Числовые характеристики: 1. M(X)=1/λ; 2. D(X)=1/λ^2 3. σ(X)=1/λ; 14. ДУ первого порядка с разделяющими переменными: P1(x)Q1(y)dx+P2(x)Q2(y)dy=0 При делении на Q1(y)P2(x) могут быть потеряны решения, если отдельно решить уравнение Q1(y)P2(x)=0 можно установить так называемые особые решения, которые могут быть получены из общего решения. Уравнение вида y’=f1(x)f2(y) также называется ДУ с разделяющими переменными.
15. Функция f(x,y) называется однородной функцией н-ной степени, если при умножении каждого ее фрагмента на t вся функция умножается на tn: f(tx,ty)=tn*f(x,y). Функция называется однородной в нулевой степени, если f(tx,ty)=f(x,y). ДУ 1-го порядка y’=f(x,y) называется однородным, если функция f(x,y) стоящая справа является однородной функцией нулевой степени. Можно показать, что любое однородное уравнение сводится к уравнению вида: y’=ϕ(y/x) (*). Полагая (y/x=u) где u, новая независимая функция сводят однородное уравнение (*) к уравнению с разделяющими переменными.
16. Уравнения вида y’+p(x)y=q(x) заданные непрерывной функцией называются линейными ДУ 1-го порядка. Метод решения: искомая функция у представляется в виде произведения 2-х новых функций u и v: y=uv, тогда y’=u’v+uv’ u’v+uv’+p(x)uv=q(x) u’v+u(v’+p(x)v)=q(x) потребуем, чтобы выражение в скобке обращалось в ноль, приходим к системе: Сначала из 1-го уравнения системы находят функцию v=v(x) это уравнение с разделяющими переменными: v’+p(x)*v=0 v’=-p(x)*v dv/dx=-p(x)*v dv/v=-p(x)dx Ln|v|=- V= Во второе уравнение системы подставляют v находим функцию u=u(x,C), обычно эта функция находится непосредственным интегрированием. В итоге y=u(x,C)*v(x)- ОР исходного уравнения. Уравнение Бернулли: y’+p(x)y=q(x)yα
17. ДУ 2-го порядка, допускающие понижение порядка: 1-ый тип: F(x,y’,y’’)=0 (т.е. сводится к уравнению более низкого порядка) с помощью замены y’=z(x) где z-новая независимая функция, тогда: y’’=z’ и уравнение 32. Рядом называется выражение вида: 2. Если ряды Un = S1,
35. Признак Лейбница (достаточный признак сходимости знакочередующихся рядов)
Знакопеременным называется рядсодержащий бесконечно много как положительных, так и отрицательных членов. Определение: Рассмотрим ряд, если сходится ряд составленный из модулей членов исходящего ряда, то исходящий ряд называется абсолютно сходящимся. Если же ряд расходится, но при этом ряд является сходящимся, то говорят, что исходный ряд условно сходится.
37. Ряд, членами которого является функция, зависящая от Х, называется функциональным рядом:
42. Пусть выполнены следующие предположения: 1. Число элементарных исходов конечно. 2. Все элементарные исходы равновозможны, тогда верны следующие классические …. Под вероятностью Р(А) событие А понимается отношение числа элементарных исходов благоприятствующие событию А общему числу всех равновозможных элементарных исходов данного испытания. Р(А)=m/n. – n – общее число элементарных исходов; m – число элементарных исходов данного события А. Обобщение классическим вероятности на бесконечное число элементарных исходов является геометрическая вероятность. Пусть равновозможные элементарные исходы являются точками органического множества G n-мерного пространства (n=1,2,3).
41. Элементарными событиями (или элементарными исходами) называется единственные возможные взаимно-исключающие исходы опыта, (неразложимые исходы опыта) обозначающие w1, w2 и т. д. А все общее исходов относится к данному опыту обозначается Ω={w1,w2,w3…} – и называется пространством элементарных исходов. Алгебра событий: 1) Суммой двух событий А и В называется событие А+В (АᶸВ), состоящее из всех элементарных принадлежащих по крайней мере одному из событий А или В. Событие А+В имеет место когда происходит хотя бы одно из событий А или В. А+В. 2) Произведение событий А или В называется событие АВ (А
47. Универсальным способом задания случайной величины Х является ее функции распределения F(x) которая определяется следующим образом: F(x)=P(X˂x) – вероятность того, что СВ Х примет значение меньше х. Свойства функции распределения: 1) 0≤F(x)≤1 2) 3) F(x) – неубывающая на всей числовой оси т. е. если х1˂х2 =˃ F(x1) ≤ F(x2) 4) P(x1≤ x ˂ x2)= F(x2) – F(x1) 5) F(x) непрерывна слева 6) P(X ≥ x) = 1 - P(X ˂ x) = 1 – F(x)
48. СВ Х называется дискретной или она принимает конечное или четное число значений.
|


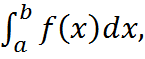 можно упростить учитывая свойства четности и нечетности функции f(x). Имеет место формула:
можно упростить учитывая свойства четности и нечетности функции f(x). Имеет место формула:
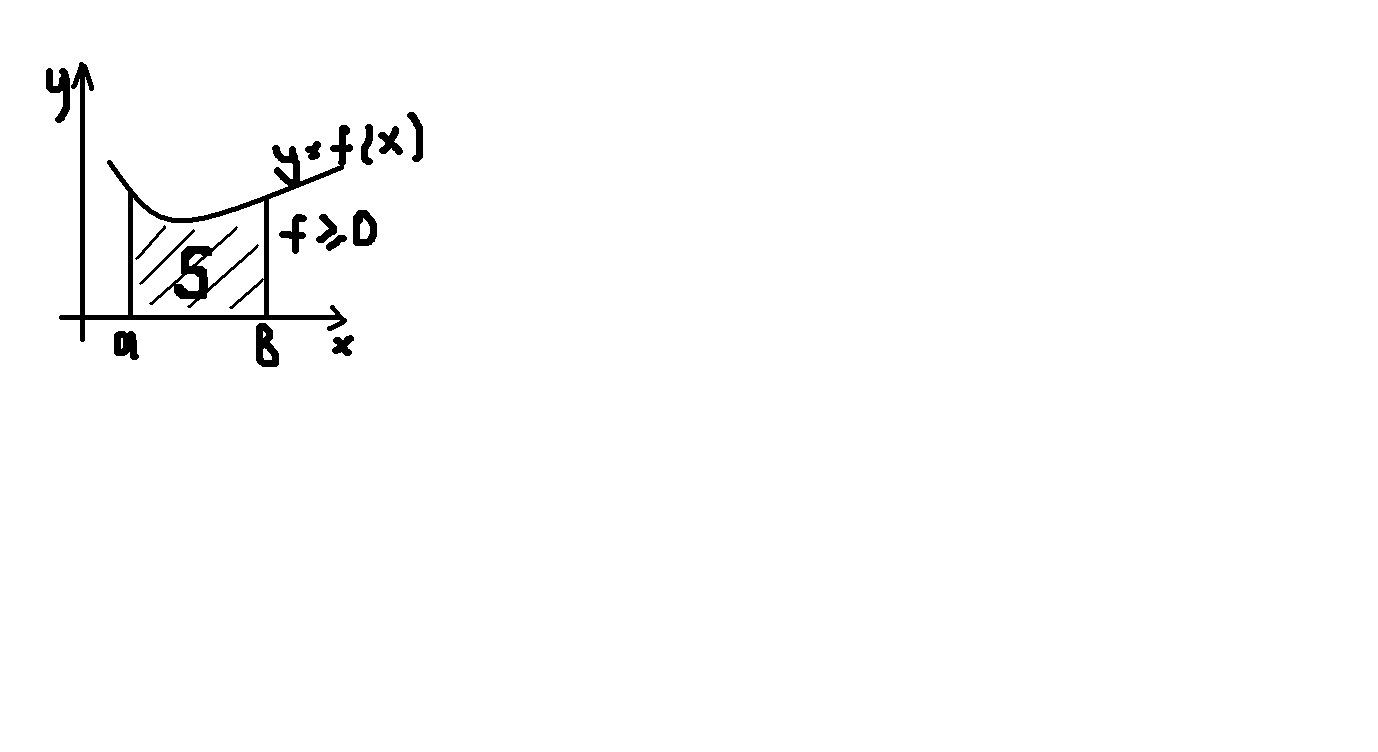
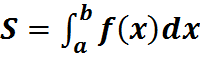
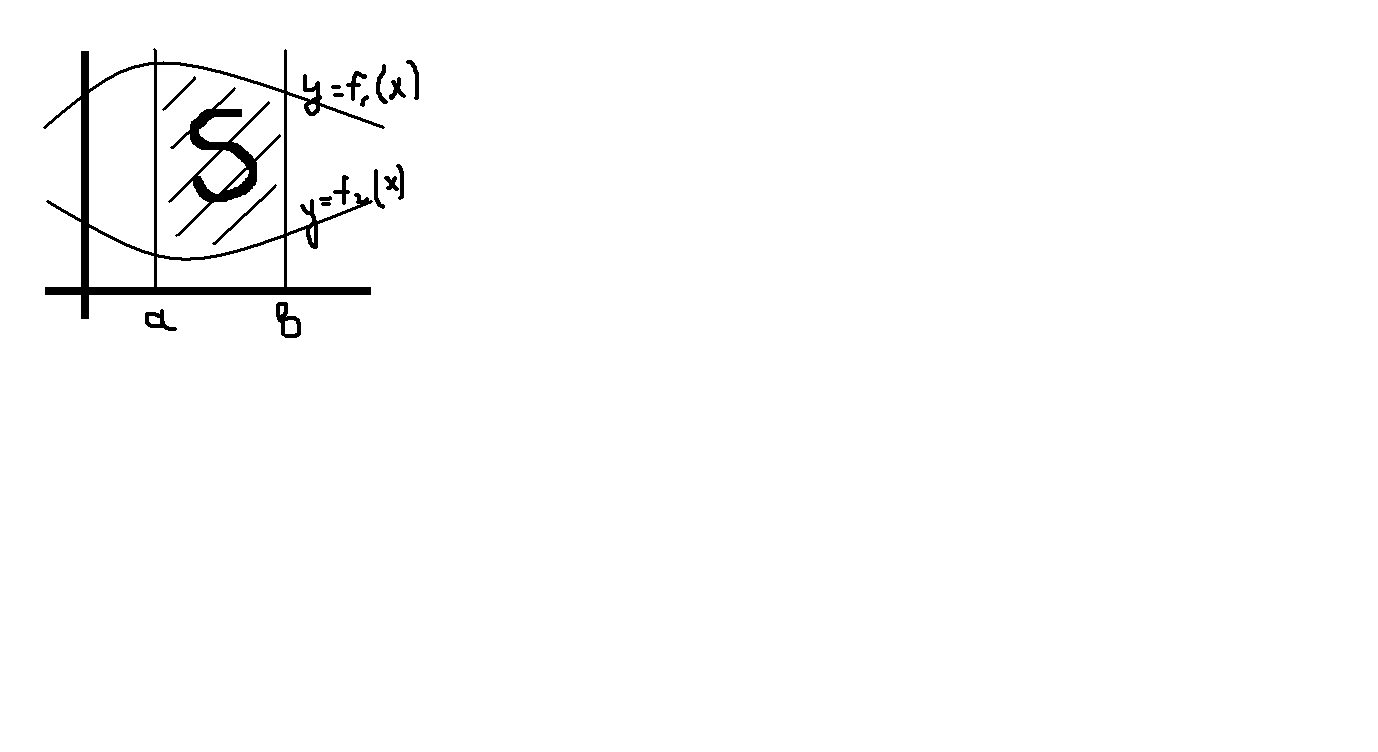
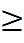 f1(x) xϵ[a,b]
f1(x) xϵ[a,b] S=
S= 


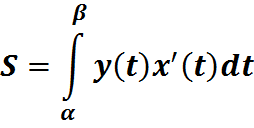

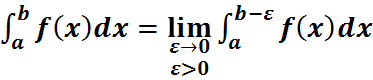 .
. следует сходимость
следует сходимость  , а из расходимости
, а из расходимости 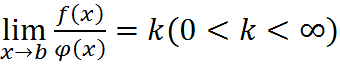 , то интегралы
, то интегралы  либо оба сходятся либо оба расходятся.
либо оба сходятся либо оба расходятся.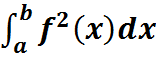 )*
)* , переходя к пределу прі n
, переходя к пределу прі n  получім формулу (*).
получім формулу (*).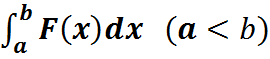
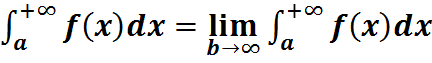 несобственный интеграл первого рода.
несобственный интеграл первого рода.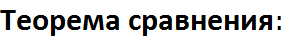 если на промежутке [a,+∞) непрерывные функции f(x), ϕ(x) удовлетворяющие условию 0≤f(x)≤ϕ(x),то из сходимости интеграла
если на промежутке [a,+∞) непрерывные функции f(x), ϕ(x) удовлетворяющие условию 0≤f(x)≤ϕ(x),то из сходимости интеграла 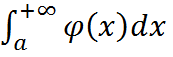 следует сходимость интеграла
следует сходимость интеграла  , а из расходимости
, а из расходимости  следует расходимость
следует расходимость  , то несобственные интегралы
, то несобственные интегралы  , либо оба сходятся либо оба расходятся.
, либо оба сходятся либо оба расходятся.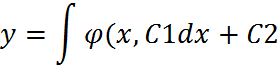
 - вронскиан (определитель Вронского).
- вронскиан (определитель Вронского).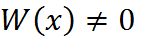 ни в одной точке (а,в), тогда и только тогда, когда функции y1(х),y2(х) линейно-независимы.
ни в одной точке (а,в), тогда и только тогда, когда функции y1(х),y2(х) линейно-независимы. /2a (
/2a (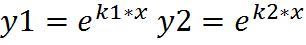 ) ОР (y=C1ek1x+C2ek2x)
) ОР (y=C1ek1x+C2ek2x) /2=α+(-)βi
/2=α+(-)βi
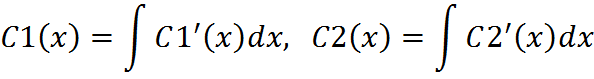
 при n→∞(λ→0) который не зависит ни от способа разбиения области Д на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x,y) по области Д и обозначается
при n→∞(λ→0) который не зависит ни от способа разбиения области Д на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x,y) по области Д и обозначается 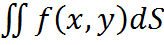 .
.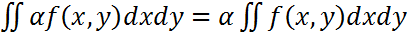

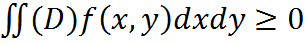 б). если f(x,y)≤g(x,y), то
б). если f(x,y)≤g(x,y), то 
 ≤M(Sd)
≤M(Sd)
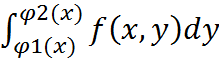 - площадь поперечного сечения цилиндрического тела.
- площадь поперечного сечения цилиндрического тела. - объем цилиндрического тела
- объем цилиндрического тела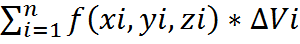 , при
, при  →∞(λ→0) независящей ни от способа разбиения области V на части, ни от выбора точек в них, то он называется тройным интегралом от функции f по области V и обозначается
→∞(λ→0) независящей ни от способа разбиения области V на части, ни от выбора точек в них, то он называется тройным интегралом от функции f по области V и обозначается 
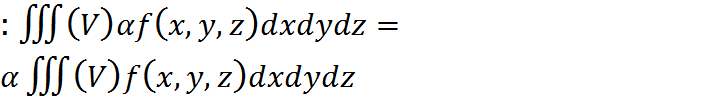


 тела
тела ценка тройного интеграла: m*V≤
ценка тройного интеграла: m*V≤ 
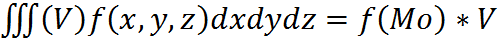
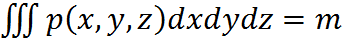 тела
тела при n→∞(λ=max
при n→∞(λ=max  →0), который не зависит ни от способа разделения кривой на части, ни от выбора точек
→0), который не зависит ни от способа разделения кривой на части, ни от выбора точек 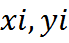 , то он называется криволинейным интегралом от функции f(x,y) по длине дуги
, то он называется криволинейным интегралом от функции f(x,y) по длине дуги 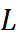 и обозначается:
и обозначается: 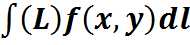
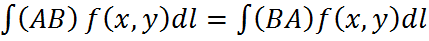
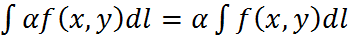


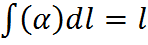 - длина дуги
- длина дуги
 , где (хс,ус)
, где (хс,ус) 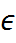 АВ
АВ
 производится в положительном направлении, когда при движении по
производится в положительном направлении, когда при движении по  расположенной в Д:
расположенной в Д: 
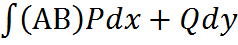 , не зависит от выбора пути интегрирования целиком лежащего в Д.
, не зависит от выбора пути интегрирования целиком лежащего в Д.
 . В каждой части произвольно выбирают точку Мi(xi,yi,zi), составляют интегральную сумму и находят ее предел называемый поверхностным интегралом(ПОВИ-1):
. В каждой части произвольно выбирают точку Мi(xi,yi,zi), составляют интегральную сумму и находят ее предел называемый поверхностным интегралом(ПОВИ-1): 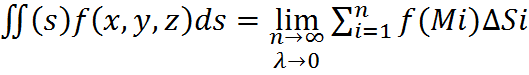
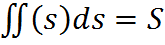 поверхности
поверхности то,
то,  поверхности
поверхности , где
, где 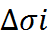 это площадь проекции соответствующей части на плоскость Оху (+)-если нормаль составляет с Оz острый угол и (-) – если тупой. В пределе при n→∞ такая сумма дает ПОВИ-2
это площадь проекции соответствующей части на плоскость Оху (+)-если нормаль составляет с Оz острый угол и (-) – если тупой. В пределе при n→∞ такая сумма дает ПОВИ-2
 (M), то говорят, что в области задано векторное поле (если рассматриваемая область на плоскости, поле называется плоским).
(M), то говорят, что в области задано векторное поле (если рассматриваемая область на плоскости, поле называется плоским).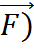 векторного поля
векторного поля  , через ориентированную поверхность S называется ПОВИ-1 скалярного произведения вектора
, через ориентированную поверхность S называется ПОВИ-1 скалярного произведения вектора 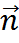 к поверхности S: ПS(
к поверхности S: ПS( 

 =
= 
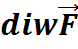 =
= 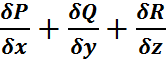 он характеризует мощность источника, если
он характеризует мощность источника, если  ˃0 в точке М и мощность стока, если
˃0 в точке М и мощность стока, если  (m)=
(m)=  = (
= (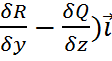 +
+ 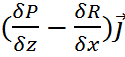 +
+ 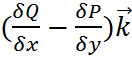
 (m)
(m)  поле называется без вихревым или потенциальным, при этом существует такая скалярная функция u(m) что grad u=
поле называется без вихревым или потенциальным, при этом существует такая скалярная функция u(m) что grad u=  , u- называется потенциалом поля.
, u- называется потенциалом поля. ,
,  причем начиная с некоторого n Un≤Vn, тогда из сходимости
причем начиная с некоторого n Un≤Vn, тогда из сходимости 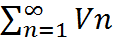 следует сходимость
следует сходимость  , тогда ряды
, тогда ряды  =l
=l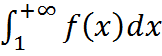 сходится, то сходится ряд
сходится, то сходится ряд 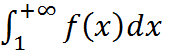 расходится, то расходится и ряд
расходится, то расходится и ряд 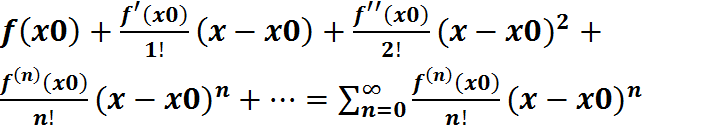
 ,причем это разложение единственно.
,причем это разложение единственно.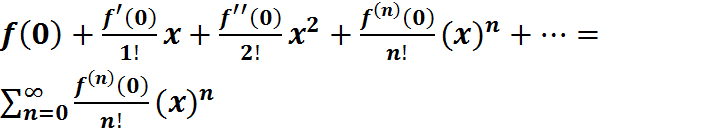
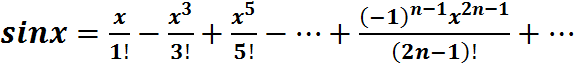


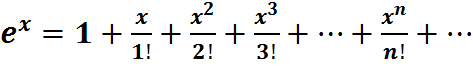


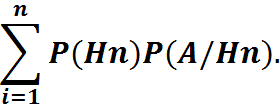
 - Формула Бернулли.
- Формула Бернулли.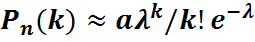 где λ=
где λ= 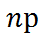 (λ≤10).
(λ≤10). *ϕ(x), где x=k-np/
*ϕ(x), где x=k-np/  , а функция имеет вид ϕ(x)=1/2π*
, а функция имеет вид ϕ(x)=1/2π* 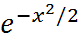 .
.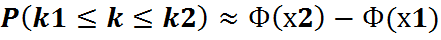 , где
, где  x2
x2  Ф(х)=
Ф(х)= 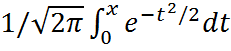 - Функция Лапласа.
- Функция Лапласа.
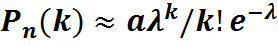

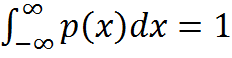
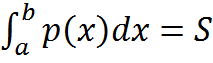
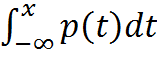
 , если он сходится.
, если он сходится.
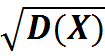

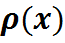 =
= 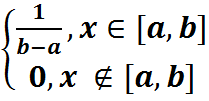

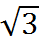
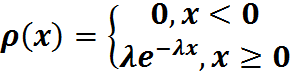 λ≥0
λ≥0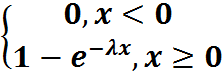

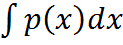
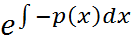
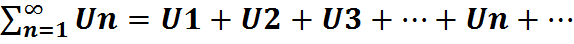
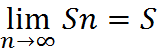 - сумма ряда.
- сумма ряда.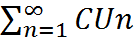 , причем его сумма = СS, где S =
, причем его сумма = СS, где S =  , то сходится и ряды
, то сходится и ряды 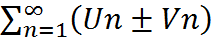 , причем
, причем 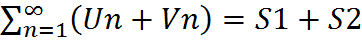 ,
, 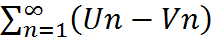 = S1-S2.
= S1-S2.

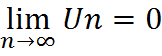 , то знакочередующийся ряд сходится, при этом сумма ряда не превосходит первого члена ряда:
, то знакочередующийся ряд сходится, при этом сумма ряда не превосходит первого члена ряда: 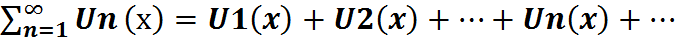
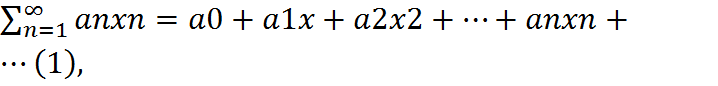 где a0,a1 и т.д. – числовые коэффициенты ряда. (х – действительная переменная)
где a0,a1 и т.д. – числовые коэффициенты ряда. (х – действительная переменная)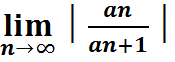
 В) состоящий из элементарных событий принадлежащих А и В одновременно. Событие А и В происходит когда происходит как событие А, так и событие В одновременно. АВ.
В) состоящий из элементарных событий принадлежащих А и В одновременно. Событие А и В происходит когда происходит как событие А, так и событие В одновременно. АВ. ,
,