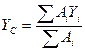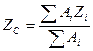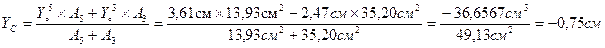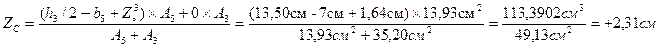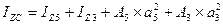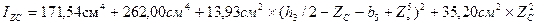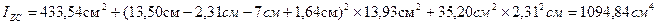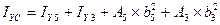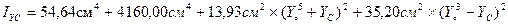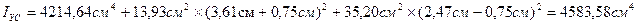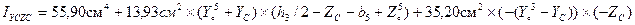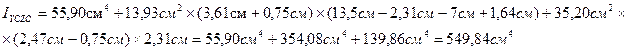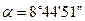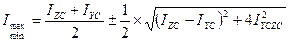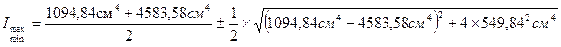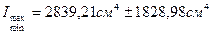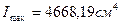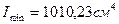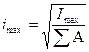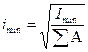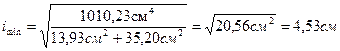Решение.
1. Меняю оси швеллера 2. Вычисляю координаты центра тяжести по формулам:
3. Определяю осевые моменты инерции сложного сечения относительно центра оси:
4. Определяем центробежный момент инерции сложного сечения относительно осей. Так как швеллер имеет ось симметрии, то для него не определяем центробежный момент инерции.
5. Определяю угол наклона относительно центральных осей:
Откуда Данный угол показываю, простив хода часовой стрелки
6. Определяю осевые моменты инерции сечения относительно главных осей по формуле:
Следовательно 7. Определяю главные радиусы инерции, которые соответствуют главным центральным осям инерции.
|

 ,
, 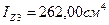 ,
,  . Выбираю вспомогательные оси сечения -
. Выбираю вспомогательные оси сечения -  ,
, 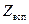 .
.