Решение транспортной задачи методом Данцига-Вулфа
Применим метод декомпозиции к Т-задаче:
"Хij³0. (6.36) Использование этого метода целесообразно, если m << n или m>>n. Оба варианта решаются идентично. Они отличаются только распределением условий между основной и вспомогательной задачами. Рассмотрим случай, когда m << n. Тогдо основная задача формируется по условиям пунктов отправления. Следовательно, множество D 0 описывается ограничениями (6.34), а D1 – условиями (6.35) и (6.36). Очевидно, что множество D1 представляет собой выпуклый многогранник (ограниченность вытекает из условий). Поэтому, как и в общем случае, любую точку в D1 можно представить в виде линейной комбинации его вершин:
S Zv =1; (6.38) " Zv ³ 0, (6.39) где Xvij – координаты v -ой вершины. Подставим (6.37) в (6.33) и (6.34):
Введем обозначения:
Тогда основная задача запишется в виде
" Zv ³ 0. (6.45) Для сбалансированной задачи условие (10) выполняется автоматически. Действительно, суммируя (6.43) и используя подстановки (6.41) и (6.35), получаем в левой части
в правой части
откуда для сбалансированной задачи следует
Поэтому при решении основной задачи условие (6.44) из модели исключается. Для определения статуса текущего базисного решения основной задачи необходимы относительные оценки. Как и в предыдущем разделе, нахождение оценок связано с решением вспомогательной задачи. Для построения вспомогательной задачи сделаем ряд преобразований: D v = pTP v - sv =
Так как основная задача решается на минимум, то оптимальному статусу соответствуют неположительные оценки. Поэтому нужно искать максимальную оценку. Если она окажется не больше нуля, то все оценки неположительны и признак оптимальности выполнился. В противном случае необходимо продолжить решение основной задачи. Значит, задача ставится так:
Вместо поиска максимума на дискретном множестве вершин
" X ij ³ 0. (6.48) Эта задача и является вспомогательной. Очевидно, что в оптимальном решении этой задачи Вспомогательная задача включает одну группу условий (6.47). Раньше было показано, что каждая переменная входит в такие условия только один раз. Поэтому равенства (6.47) оказываются независимыми и, следовательно, вспомогательная задача распадается на n простейших независимых задач, каждая из которых имеет всего одно условие:
" X ij ³ 0. (6.51) Критерий вспомогательной задачи равен сумме критериев этих задач:
Оптимальное решение задачи (6.49)-(6.51), как линейной, находится на границе. При этом только одна переменная не равна нулю (базис имеет размерность 1). Поэтому ее решение состоит в определении максимального коэффициета в критерии (6.49). Пусть максимум достигается на индексе i*, то есть
Тогда имеем следующее решение задачи (6.49)-(6.51): Xvi*j = bj, Xvij =0, " i, i ¹ i*, (6.53) и максимальная оценка определится как
Если L * всп £ 0, то положительных оценок нет и текущее решение основной задачи будет оптимальным. При L*всп > 0 начинается новая итерация: 1. пo (6.41) и (6.40) находим Р v и sv; 2. вычисляем элементы направляющего столбца как коэффициенты разложения вектора Р v по текущему базису: a v = P -1B P v; 3. проводим симплекс-преобразование основной задачи, в результате которого получаем новое решение и новую обратную матрицу; 4. вычисляем p T= s TB P -1B; 5. решаем вспомогательную задачу: вычисляем разности Из рассмотренной вычислительной схемы следует, что эффективность метода тем выше, чем сильнее неравенство m << n или m>>n. Пример. Решим транспортную задачу с двумя пунктами отправления и четырьмя пунктами назначения:
Числа в ячейках таблицы - затраты на перевозки Cij. Исходная модель задачи: L = SS CijXij àmin
Координирующая задача формируется по условиям (6.54):
" Zv ³0. Для построения начального решения вводим искусственные переменные:
и модифицируем критерий
Составим начальную таблицу координирующей задачи:
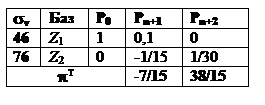
В последней строке значения pi получены умножением первого столбца на столбцы P n+i. Решение вспомогательной задачи представляем в таблице:
Значения переменных в последней строке таблицы получены согласно (6.53). Например, при j =1 максимальная разность равна M -1, поэтому X121 = b1 =8. Клетки с максимальными разностями выделены цветом фона. Вычисляем значение критерия по формуле (6.46):
Так как признак оптимальности не выполняется, переходим к итерациям. Находим s1 согласно (6.40): s 1=1*8 + 3*4 + 1*10 + 2*8 = 46. Вычисляем компоненты вектора Р 1: Р 11= X1 13=10; P 21= X1 21+ X1 2 2 + X1 24= 8+4+8 = 20. Следовательно,
Добавляем столбец P 1с элементами a 1 в начальную таблицу в качестве направляющего столбца:
Взяв 1-ю строку за направляющую и выполнив симплекс-преобразование, получаем новое решение основной задачи: Для выяснения статуса этого решения снова находим максимальную оценку основной задачи, решая вспомогательную задачу:
Очевидно, что L2всп>0, то есть решение основной задачи не является оптимальным. Вычисляем коэффициент критерия при Z 2: s 2=1*8 + 3*4 + 4*10 + 2*8 = 8+12+40+16 = 76. Определяем компоненты вектора Р 2: Р 12=0, P22 = 8+4+10+8 = 30 Имея
и добавляем его к последней таблице основной задачи:
В результате симплекс-преобразования получаем:
Соответствующая вспомогательная задача: Критерий этой заачи L 3 всп =(23/15)*8–(7/15)*4–(22/15)*10+(8/15)*8=0. Следовательно, получено оптимальное решение основной задачи: Z* 1=1, Z* 2=0, L* = 46*1 + 76*0 = 46. Находим значения исходных переменных по формуле (6.37), которая для нашей задачи принимает вид:
Таким образом, получено следующее оптимальное решение исходной задачи: X* 21 = 8, X* 22 = 4, X* 13 = 10, X* 24 = 8. Проверка: L = SS CijXij =1*8 + 3*4 + 1*10 + 2*8=46. Это значение совпадает с вычисленным через переменные Zi.
6.3. Задания для самостоятельной работы Транспортные задачи решить методом декомпозиции Данцига-Вулфа.
1 2
3 4
5 6
7 8
9 10
11 12
13 14
15 16
|

 (6.33)
(6.33)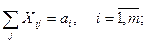 (6.34)
(6.34)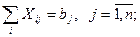 (6.35)
(6.35)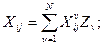 (6.37)
(6.37)
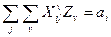 .
. (6.40)
(6.40) (6.41)
(6.41) (6.42)
(6.42) 6.43)
6.43) (6.44)
(6.44)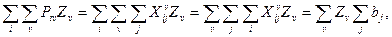
 Таким образом,
Таким образом,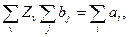



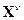 перейдем к эквивалентной задаче поиска на всем непрерывном множестве D1:
перейдем к эквивалентной задаче поиска на всем непрерывном множестве D1: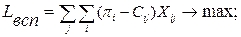 (6.46)
(6.46)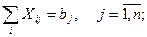 (6.47)
(6.47) Теперь остается выяснить, как найти его.
Теперь остается выяснить, как найти его. (6.49)
(6.49) (6.50)
(6.50)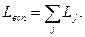 (6.52)
(6.52)
 .
. , находим оптимальные решения n задач (6.49)-(6.51) и максимальную оценку основной задачи.
, находим оптимальные решения n задач (6.49)-(6.51) и максимальную оценку основной задачи. (6.54)
(6.54) (6.55)
(6.55)
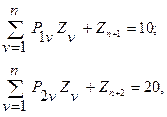

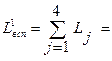 [(M -1)*8 + (M -3)*4 + (M -1)*10 + (M -2)*8] > 0.
[(M -1)*8 + (M -3)*4 + (M -1)*10 + (M -2)*8] > 0.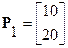 . Находим его разложение по начальному базису:
. Находим его разложение по начальному базису: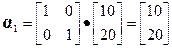 .
.

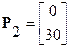 , находим элементы направляющего столбца
, находим элементы направляющего столбца