Расчет прочности ребристой плиты по сечению, наклонному к продольной оси.
Расчетная поперечная сила - Влияние продольных усилий обжатия
Проверяем, требуется ли поперечная арматура по расчету:
При Вычислим значение
Принимаем Проверяем условие, при котором не требуется установка арматуры:
На при опорном участке длинной
4.8. Расчет многопустотной плиты по предельным состояниям второй группы. Определение геометрических характеристик приведенного сечения Круглое сечение пустот заменяем эквивалентными квадратами со стороной Толщина полок эквивалентного сечения Широна ребра 96-6*12,6=20,4 см Ширина пустот 96-20,4=75,6см Площадь приведенного сечения:
Находим расстояние от нижней грани до центра тяжести приведенного сечения: Момент инерции приведенного сечения плиты относительно центра тяжести: Момент сопротивления приведенного сечения по верхней и нижней зоне:
Момент сопротивления приведенного сечения по верхней зоне:
Расстояние от ядровой точки, наиболее удаленной от растянутой (верхней) зоны до центра тяжести приведенного сечения согласно формуле:
Отношение напряжения в бетоне от нормативных нагрузок и усиления обжатия к расчетному сопротивлению бетона для предельных состояний 2-й группы предварительно принимают равным 0,75. Упруго - пластический момент сопротивления в растянутой зоне согласно формуле Упруго - пластический момент сопротивления в растянутой зоне в стадии изготовления и обжатия элемента 4.9. Определение потерь предварительного напряжения в арматуре. Коэффициент точности натяжения арматуры Потери от температурного перепада между натянутой арматурой и упорами Усилия обжатия Эксцентриситет этого усилия относительно центра тяжести приведенного сечения Напряжения в бетоне при обжатии в соответствии с формулой
Устанавливают передаточную прочность бетона из условия:
Вычисляем сжимающие напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия Р1. Тогда Потери от быстро натекающей ползучести Первые потери С учетом потерь Полные потери Усилие обжатия с учетом полных потерь:
4.10. Расчет по образованию трещин, нормальных к продольной оси. Выполняем проверку для выяснения необходимости расчета по раскрытию трещин. Для элементов, к трещиностойкости которых предъявляют требования третьей категории, принимают значение коэффициента надежности по нагрузке Определяем момент образования трещин по приближенному способу:
Проверяем, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения
Расчетное условие:
4.11. Расчет по раскрытию трещин, нормальных к продольной оси при gsp=1. Предельная ширина раскрытия трещин: Непродолжительная - Продолжительная - Изгибающий момент от нормативных нагрузок: Постоянной и длительной – М=34,39кН´м; Полной – М=40,9 кН´м. Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок:
Приращение напряжений в арматуре от действия полной нагрузки:
Вычисляем ширину раскрытия трещин от непродолжительного действия полной нагрузки:
Ширину раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок:
Ширину раскрытия трещин от постоянной и длительной нагрузок:
Непродолжительная ширина раскрытия трещин:
Предположительная ширина раскрытия трещин - 4.12. Расчет прогиба плиты. Определяем предельный прогиб: Вычисляем параметры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузки – М=34.39 кН´м. Суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при
Коэффициент, характеризующий неравномерности деформаций растянутой арматуры на участках между трещинами:
Вычислим кривизну оси при изгибе:
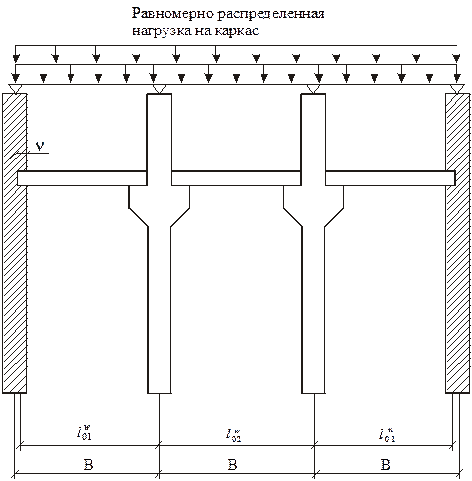
Вычисляем прогиб по формуле: Значение полученного прогиба не превышает предельного максимально допустимого значения. 5. Расчет железобетонного ригеля перекрытия. 5.1. Расчетная схема неразрезного ригеля. Для проектируемого многоэтажного здания принята конструктивна схема с неполным каркасом. В соответствии с конструктивной схемой каркаса здания в крайних пролетах ригеля расчетная длинна принимается равной расстоянию ото оси опоры балки на кирпичной стене, до оси ближайшей колонны. Расчетная длинна среднего ригеля равна расстоянию между геометрическими осями соседних колонн:
В=6 метрам – расстояние между поперечными разбивочными осями.
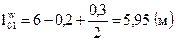 ; ; 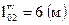 . .
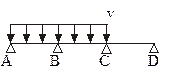
Рис. 24 Расчетная схема здания с неполным каркасом. Нагрузка на ригель от ребристой плиты считается равномерно распределенной. Ширина грузовой полосы на ригель равна шагу поперечных рам, в нашем случае – 7 метров. 5.2. Определение расчетных нагрузок. Произведен расчет нагрузок на 1 м2 перекрытия, результат расчета сведен в таблицу №3. Сбор нагрузок на 1 м2 перекрытия.
Определяем расчетную нагрузку на 1 м длинны ригеля: Постоянная: от перекрытия с учетом коэффициента надежности по назначению здания
От веса ригеля сечением 0,25´0,6 м ( Итого: Временная: с учетом коэффициента надежности по назначению в том числе длительная: кратковременная: Полная нагрузка:
5.3. Определение изгибающих моментов в расчетных сечениях ригеля. Результаты вычисления опорных и пролетных моментов приведены в табличной форме в таблице №4. 5.4. Перераспределение моментов под влиянием образования пластических шарниров в ригеле. Практически перераспределение изгибающих моментов под влиянием пластических деформаций заключается в уменьшении примерно на 30% опорного момента Мb, соответствующего схемам загружения 1+4. К эпюре моментов по схеме 1+4 добавляется треугольная выравнивающая эпюра с максимальной ординатой
Таблица №4. Опорные и пролетные моменты от различного вида загружения.
По данным таблицы 4 строятся эпюры изгибающих моментов и поперечных сил при различных комбинациях схем загружения. При этом постоянная нагрузка по схеме I участвует во всех комбинациях: 1+2; 1+3; 1+4. Построение эпюры моментов, рассчитанной по упругой схеме для комбинации нагрузок.
Рис. Огибающая эпюра и эпюра поперечных сил. Построение эпюры моментов, рассчитанной по упругой схеме для комбинации нагрузок.
Рис. Огибающая эпюра и эпюра поперечных сил. Построение эпюры моментов, рассчитанной по упругой схеме для комбинации нагрузок.
Рис. Огибающая эпюра и эпюра поперечных сил. 5.5. Вычисление моментов в ригеле по грани колонны. Расчетными на опоре являются сечения ригеля по грани колонны. В этих сечениях максимальные изгибающие моменты определяются по формуле:
На опоре В при схеме загружения 1+4 опорный момент по грани колонны не всегда оказывается расчетным, максимальным по абсолютному значению. Он может оказаться расчетным при схеме загружения 1+2 или 1+3. Поэтому необходимо определить моменты по всем схемам загружения.
|

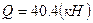 .
.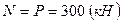 (смотри расчет предварительных напряжений арматуры плиты).
(смотри расчет предварительных напряжений арматуры плиты).

 - удовлетворяется.
- удовлетворяется.

 .
.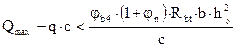 ;
;  .
. ,
,  - условие не соблюдается, следовательно, поперечная арматура требуется по расчету.
- условие не соблюдается, следовательно, поперечная арматура требуется по расчету. устанавливают в каждом ребре плиты поперечные стержни Æ4 Вр-1 с шагом
устанавливают в каждом ребре плиты поперечные стержни Æ4 Вр-1 с шагом 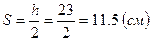 , в средней части пролета с шагом
, в средней части пролета с шагом  .
.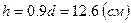
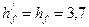
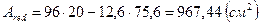
 .
.


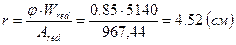 , то же, наименее удаленной от растянутой зоны (нижней):
, то же, наименее удаленной от растянутой зоны (нижней):  , где
, где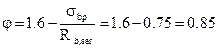 .
.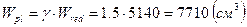 ; где
; где  =1,5 для двутаврового сечения.
=1,5 для двутаврового сечения. , при
, при 
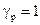 . Потери от релаксации напряжений в арматуре при электротермическом способе натяжения
. Потери от релаксации напряжений в арматуре при электротермическом способе натяжения 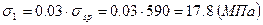 .
. , так как при пропаривании форма с упорами нагревается вместе с изделиями.
, так как при пропаривании форма с упорами нагревается вместе с изделиями.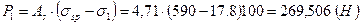 .
. .
.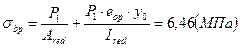 .
.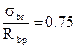 ;
;  ; принимаем Rbp равной 14.5 МПа.тогда
; принимаем Rbp равной 14.5 МПа.тогда 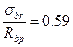 .
.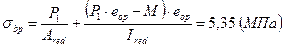
 и при
и при  составляют
составляют  .
. .
. напряжения
напряжения  Потери от осадки бетона
Потери от осадки бетона 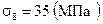 . Потери от ползучести бетона при
. Потери от ползучести бетона при  составляют
составляют 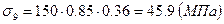 . Вторые потери
. Вторые потери 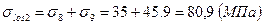 .
.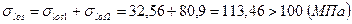 , то есть больше установленного минимального значения потерь.
, то есть больше установленного минимального значения потерь.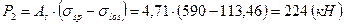
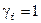 ;
; 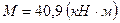 . Условием, при котором не образуются трещины является условие - если момент внешних сил не превосходит момента внутренних усилий в сечении перед образованием трещины
. Условием, при котором не образуются трещины является условие - если момент внешних сил не превосходит момента внутренних усилий в сечении перед образованием трещины  , то есть
, то есть 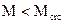 .
.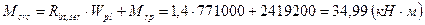
 , где
, где  .
.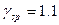

 ,
,  <
< 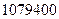 – условие выполняется, начальные трещины не образуются;
– условие выполняется, начальные трещины не образуются;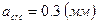 ;
;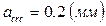 .
.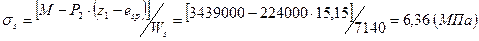 , где
, где - плечо внутренней пары сил;
- плечо внутренней пары сил;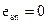 - так как усилие обжатия Р приложено к центру тяжести сечения нижней напрягаемой арматуры;
- так как усилие обжатия Р приложено к центру тяжести сечения нижней напрягаемой арматуры;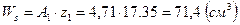 - момент сопротивления сечения по растянутой арматуре.
- момент сопротивления сечения по растянутой арматуре. .
. , где
, где 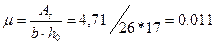 ;
; 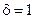 ;
; 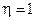 ;
;  ;
; 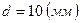 - диаметр продольной арматуры.
- диаметр продольной арматуры. .
.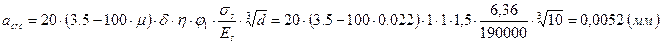 , где
, где  .
. .
.
 .
.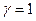 :
: ; эксцентриситет
; эксцентриситет 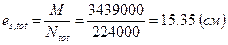 ; коэффициент
; коэффициент  - при длительном действии нагрузки.
- при длительном действии нагрузки.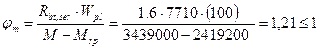 .
.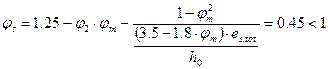 .
.



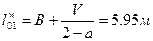 ;
;  .
.
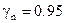 .
.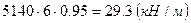 .
.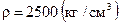 ) с учетом коэффициента надежности
) с учетом коэффициента надежности 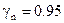 и
и 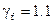 равна 3.92 кН/м.
равна 3.92 кН/м. .
.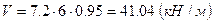 ;
;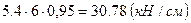
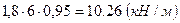 .
.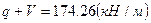

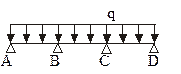


 , где
, где 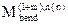 - граневый изгибающий момент у опоры В слева (л) или справа (п) от нее при схеме загружения 1+m(m=2.3.4).
- граневый изгибающий момент у опоры В слева (л) или справа (п) от нее при схеме загружения 1+m(m=2.3.4).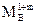 - изгибающий момент на опоре В.
- изгибающий момент на опоре В.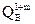 - поперечная сила на опоре В справа (п) или слева (л) от нее.
- поперечная сила на опоре В справа (п) или слева (л) от нее.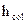 - размер поперечного сечения колонны
- размер поперечного сечения колонны


