Ур-ние прогиба фундаментных балок опирающихся на сплошное упругое основание, по теории местных деформаций выводится из условия совместной работы фундаментной балки и упругого основания 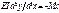 - ур-ние изогнутой оси балки, EI – жесткость фундаментной балки, М – изгибающий моментот действия внешней силы.
- ур-ние изогнутой оси балки, EI – жесткость фундаментной балки, М – изгибающий моментот действия внешней силы. 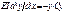 - ДУ изгиба балок на упругом основании по теории местных упругих деформаций. Решение данного ур-ния записывается виде
- ДУ изгиба балок на упругом основании по теории местных упругих деформаций. Решение данного ур-ния записывается виде  , где х – координата длины, у – прогиб балки, с1-с4 –пост интегрирования, а- коэф-нт
, где х – координата длины, у – прогиб балки, с1-с4 –пост интегрирования, а- коэф-нт
87. Расчет фундаментных балок и плит на линейно деформируемом полупространстве: - бесконечно жесткие полосы; - гибкие полосы конечной жесткости.
1.При центральной нагрузке реактивное давление Px грунта на фундамент определяется по 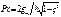 , где qm – среднее давление на единицу площади фундамента, ζ =х/е – координата относительная. Проинтегрировав последовательно выражение по Px мы получим выражение для перерезывающей силы и изгибающего момента или усилия для расчета балки.
, где qm – среднее давление на единицу площади фундамента, ζ =х/е – координата относительная. Проинтегрировав последовательно выражение по Px мы получим выражение для перерезывающей силы и изгибающего момента или усилия для расчета балки.
2. Это методы в основу которых положены турбулентные решения, а также практические методы Жемочкина. Метод Горбун-Пос. дает завышение внешних изгибающих моментов. По методу Симвул составлено большое кол-во таблиц, в которых описывается почти все расчетные случаи. По методу Горб – Пос осущ совместное решение путем применения одиночного или двойного степ рядов и ур-ния деф-ии грунтового основания как линейно деформируемого полупространства. Для этого метода исх данными являются ДУ изгиба полосы в приведенных координатах. И выражение для осадок линейно деф-ого полупространства от действия равномерно распределенной нагрузки. Согласно методу дает распределение реактивных давлений основания по закону бесконечно степенного ряда с заменой полинома 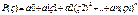 , коэф-нты а – опр из условий равновесия и равенства прогибов балки. Решения представлены в виде таблиц реактивных давлений P,Q, M. Метод Симулиди: на основании анализа ДУ изогнутой оси балки и ур-ния деформаций основания предложил для определения реакций основания полином 3-й степени
, коэф-нты а – опр из условий равновесия и равенства прогибов балки. Решения представлены в виде таблиц реактивных давлений P,Q, M. Метод Симулиди: на основании анализа ДУ изогнутой оси балки и ур-ния деформаций основания предложил для определения реакций основания полином 3-й степени 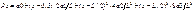 , где а – параметр зависящий от св-в основания, размеров и жесткости ф-та, х – корд длины, за начало левый конец балки, L – длина балки. Составляется 8 ур-ний с 8 неизвестными. По результатам расчета составляем таблицы по определению коэ-тов по описанию P, Q, M. Метод Жемочкина: в методе используются следующие допущения: - распределение реактивных усилий по подошве ф-тной балки принимается ступенчатым, причем ступени имеют одинаковую длину, а число их зависит от точности расчета; - в пределах каждой ступени реакция грунта усредняется по длине ступени и заменяется шарнирными стержнями приложенными в середине участка; - полученные стержневые с-мы опираются на ряд жестких шарнирных стержней, рассматриваемых как фундаментная балка лежащая на сплошном линейно деф-мом основании; - условие совместной работы балки и основания, равенство прогибов балки и осадки основания в месте закрепления стержней. Составляется с-ма ур-ний, решив которое получим x1, x2 xn. Зная их можно получить вспышку реактивного давления P1, Р2, Р3: P1=Х1/С. Зная реактивное давление осно-ния может получить значение перерезывающих сил Qx и Y/
, где а – параметр зависящий от св-в основания, размеров и жесткости ф-та, х – корд длины, за начало левый конец балки, L – длина балки. Составляется 8 ур-ний с 8 неизвестными. По результатам расчета составляем таблицы по определению коэ-тов по описанию P, Q, M. Метод Жемочкина: в методе используются следующие допущения: - распределение реактивных усилий по подошве ф-тной балки принимается ступенчатым, причем ступени имеют одинаковую длину, а число их зависит от точности расчета; - в пределах каждой ступени реакция грунта усредняется по длине ступени и заменяется шарнирными стержнями приложенными в середине участка; - полученные стержневые с-мы опираются на ряд жестких шарнирных стержней, рассматриваемых как фундаментная балка лежащая на сплошном линейно деф-мом основании; - условие совместной работы балки и основания, равенство прогибов балки и осадки основания в месте закрепления стержней. Составляется с-ма ур-ний, решив которое получим x1, x2 xn. Зная их можно получить вспышку реактивного давления P1, Р2, Р3: P1=Х1/С. Зная реактивное давление осно-ния может получить значение перерезывающих сил Qx и Y/

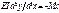 - ур-ние изогнутой оси балки, EI – жесткость фундаментной балки, М – изгибающий моментот действия внешней силы.
- ур-ние изогнутой оси балки, EI – жесткость фундаментной балки, М – изгибающий моментот действия внешней силы. 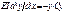 - ДУ изгиба балок на упругом основании по теории местных упругих деформаций. Решение данного ур-ния записывается виде
- ДУ изгиба балок на упругом основании по теории местных упругих деформаций. Решение данного ур-ния записывается виде  , где х – координата длины, у – прогиб балки, с1-с4 –пост интегрирования, а- коэф-нт
, где х – координата длины, у – прогиб балки, с1-с4 –пост интегрирования, а- коэф-нт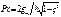 , где qm – среднее давление на единицу площади фундамента, ζ =х/е – координата относительная. Проинтегрировав последовательно выражение по Px мы получим выражение для перерезывающей силы и изгибающего момента или усилия для расчета балки.
, где qm – среднее давление на единицу площади фундамента, ζ =х/е – координата относительная. Проинтегрировав последовательно выражение по Px мы получим выражение для перерезывающей силы и изгибающего момента или усилия для расчета балки.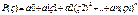 , коэф-нты а – опр из условий равновесия и равенства прогибов балки. Решения представлены в виде таблиц реактивных давлений P,Q, M. Метод Симулиди: на основании анализа ДУ изогнутой оси балки и ур-ния деформаций основания предложил для определения реакций основания полином 3-й степени
, коэф-нты а – опр из условий равновесия и равенства прогибов балки. Решения представлены в виде таблиц реактивных давлений P,Q, M. Метод Симулиди: на основании анализа ДУ изогнутой оси балки и ур-ния деформаций основания предложил для определения реакций основания полином 3-й степени 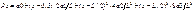 , где а – параметр зависящий от св-в основания, размеров и жесткости ф-та, х – корд длины, за начало левый конец балки, L – длина балки. Составляется 8 ур-ний с 8 неизвестными. По результатам расчета составляем таблицы по определению коэ-тов по описанию P, Q, M. Метод Жемочкина: в методе используются следующие допущения: - распределение реактивных усилий по подошве ф-тной балки принимается ступенчатым, причем ступени имеют одинаковую длину, а число их зависит от точности расчета; - в пределах каждой ступени реакция грунта усредняется по длине ступени и заменяется шарнирными стержнями приложенными в середине участка; - полученные стержневые с-мы опираются на ряд жестких шарнирных стержней, рассматриваемых как фундаментная балка лежащая на сплошном линейно деф-мом основании; - условие совместной работы балки и основания, равенство прогибов балки и осадки основания в месте закрепления стержней. Составляется с-ма ур-ний, решив которое получим x1, x2 xn. Зная их можно получить вспышку реактивного давления P1, Р2, Р3: P1=Х1/С. Зная реактивное давление осно-ния может получить значение перерезывающих сил Qx и Y/
, где а – параметр зависящий от св-в основания, размеров и жесткости ф-та, х – корд длины, за начало левый конец балки, L – длина балки. Составляется 8 ур-ний с 8 неизвестными. По результатам расчета составляем таблицы по определению коэ-тов по описанию P, Q, M. Метод Жемочкина: в методе используются следующие допущения: - распределение реактивных усилий по подошве ф-тной балки принимается ступенчатым, причем ступени имеют одинаковую длину, а число их зависит от точности расчета; - в пределах каждой ступени реакция грунта усредняется по длине ступени и заменяется шарнирными стержнями приложенными в середине участка; - полученные стержневые с-мы опираются на ряд жестких шарнирных стержней, рассматриваемых как фундаментная балка лежащая на сплошном линейно деф-мом основании; - условие совместной работы балки и основания, равенство прогибов балки и осадки основания в месте закрепления стержней. Составляется с-ма ур-ний, решив которое получим x1, x2 xn. Зная их можно получить вспышку реактивного давления P1, Р2, Р3: P1=Х1/С. Зная реактивное давление осно-ния может получить значение перерезывающих сил Qx и Y/


