Дана система належить до багатоканальних систем масового обслуговування з відмовами.
Багатоканальні СМО – це СМО з декількома однаковими пристроями обслуговування, що ввімкнені паралельно (мал. 2.4).
Аналіз багатоканальних СМО набагато складніший, ніж одноканальних. За допомогою теорії масового обслуговування можна отримувати аналітичні залежності в замкнутому вигляді для розрахунку характеристик роботи багатоканальних СМО в стаціонарному режимі роботи тільки лише для моделей типу Для системи, що складається з
Його можна трактувати як математичне очікування числа зайнятих пристроїв. Розглянемо класичне завдання Эрланга. Є п каналів, на які поступає потік заявок з інтенсивністю Система S (СМО) має наступні стани (нумеруємо їх по числу заявок, що знаходяться в системі): So, S1, S2,..., Sk..., Sn, де Sk — стан системи, коли в ній знаходиться k заявок, тобто зайнято k каналів. Граф станів СМО відповідає процесу загибелі і розмноження показаний на мал. 2
   … … 
Мал. 2
Потік заявок послідовно переводить систему з будь-якого лівого стану в сусідній правий з однією і тією ж інтенсивністю Для схеми загибелі і розмноження одержимо для граничної вірогідності стану
де члени розкладання Величина
Формула (а) для граничної вірогідності одержала назву формула Эрланга на честь засновника теорії масового обслуговування. Вірогідність відмови СМО є гранична вірогідність того що всі п каналів системи будуть зайняті, тобто
Відносна пропускна спроможність — вірогідність того, що заявка буде обслужена:
Середнє число зайнятих каналів є математичне очікування числа зайнятих каналів:
де pk — гранична вірогідність станів, визначуваних по формулі (8). Проте середнє число зайнятих каналів можна знайти простіше, якщо врахувати, що абсолютна пропускна спроможність системи А є не що інше, як інтенсивність потоку обслужених системою заявок (у одиницю часу). Оскільки кожен зайнятий канал обслуговує в середньому заявок (у одиницю часу), то середнє число зайнятих каналів
або
Складаємо ланцюг Маркова для даної системи:
Вихідні параметри: λ=0,7;r=3; µ=3
Висновок:
як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%.
|

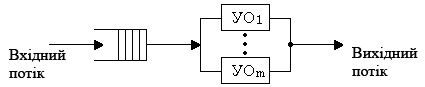
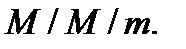 Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи.
Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи.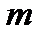 однакових пристроїв обслуговування коефіцієнт завантаження дорівнює:
однакових пристроїв обслуговування коефіцієнт завантаження дорівнює: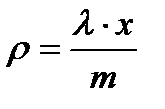
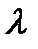 . Потік обслуговувань має інтенсивність
. Потік обслуговувань має інтенсивність 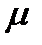 . Знайти граничну вірогідність станів системи і показники її ефективності.
. Знайти граничну вірогідність станів системи і показники її ефективності.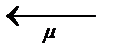
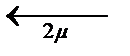
 …
… 

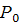 називається приведеною інтенсивністю потоку заявок або інтенсивністю навантаження каналу. Вона виражає середнє число заявок, що приходить за середній час обслуговування однієї заявки. Тепер
називається приведеною інтенсивністю потоку заявок або інтенсивністю навантаження каналу. Вона виражає середнє число заявок, що приходить за середній час обслуговування однієї заявки. Тепер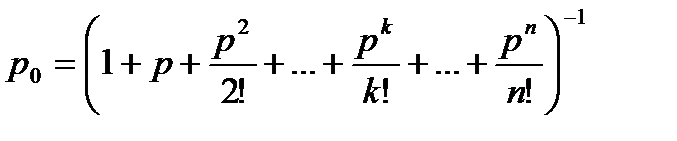 (а)
(а)
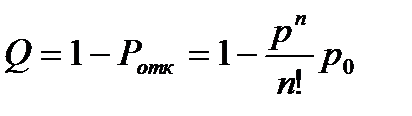
 Абсолютна пропускна спроможність:
Абсолютна пропускна спроможність: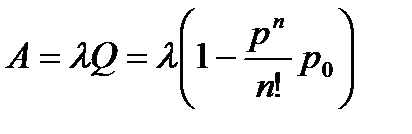

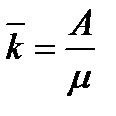

















 7,8%
7,8%






