И характеристики диодного детектора
Схема амплитудного диодного детектора изображена на рис. 5.1. На вход детектора поступает высокочастотный сигнал u c(t). Детектор представляет собой последовательное соединение диода VD и нагрузочной цепи (фильтра): конденсатора С ни резистора R н, включенных параллельно. С нагрузочной цепи снимается выходное колебание u вых(t). Значение тока через диод ig для режима покоя u c(t) = 0 может быть найдено из уравнений
где Ug – напряжение на диоде VD (см. рис. 5.1). Первое уравнение – это уравнение вольт-амперной характеристики (ВАХ) диода как безынерционного нелинейного элемента. Из-за нелинейного характера ВАХ форма тока через диод ig при синусоидальной форме сигнала u c(t) не является синусоидальной. В токе появляется постоянная составляющая, которая, протекая по резистору R н, создает падение напряжения U =, смещающее положение рабочей точки. При увеличении амплитуды входного напряжения смещение рабочей точки возрастает и ток через диод будет приближаться по форме к однополярным импульсам, открывающим диод при положительных значениях входного напряжения.
Рис. 5.2. Детектирование амплитудно-модулированных сигналов
На рис. 5.2 приведены формы напряжений и токов на входе детектора для двух случаев, когда амплитуды входных сигналов удовлетворяют неравенству U c(1) < U c(2). Тогда постоянные составляющие напряжений U =(1) < U =(2) и I =(1) < I =(2). На этом же рисунке условно изображена зависимость ig = f (t). Вольт-амперная характеристика диода в широком диапазоне токов достаточно точно аппроксимируется экспоненциальной зависимостью:
где I об– абсолютное значение величины обратного тока диода; φT– температурный потенциал, равный 26 мВ при Т = 300 K. Полагая напряжение на диоде равным ug (t) = u a(t)cos(ωc t) – U = , подставляя ug (t)в выражение (4.6) и раскладывая в ряд по функциям Бесселя Jk, получаем
Выделим в выражении (5.7) компоненты токов – постоянный I =, переменный I ω с частотой ωc, переменный I 2ω с частотой 2ωc:
Как уже отмечалось, зависимость постоянной составляющей U = от амплитуды приложенного напряжения U cназывается детекторной характеристикой (рис. 5.3). Из выражений (5.8) и (5.1) следует, что при x (t) = 0 детекторная характеристика может быть записана в виде
Анализ выражения (5.9) позволяет сделать два основных вывода: § с увеличением R нвозрастает крутизна детекторной характеристики; § с увеличением уровня сигнала уменьшается степень нелинейности детекторной характеристики, и наоборот, детектирование «слабых» сигналов сопровождается значительными нелинейными искажениями закона модуляции. В этой связи различают два режима работы диодного амплитудного детектора: детектирование «слабых» сигналов и детектирование «сильных» сигналов. В режиме «слабых» сигналов, представив функцию J 0(u a(t)/φT) в виде ряда, нетрудно показать, что детекторная характеристика имеет квадратичный вид, т. е.
и, соответственно, коэффициент нелинейных искажений в этом случае при x (t) = 0 равен
Допустимое значение k н, например в системах радиовещания, не превышает нескольких процентов (k н £ 5 %), что налагает ограничения на допустимый коэффициент глубины амплитудной модуляции в передатчике. Дополнительным недостатком работы на квадратичном участке детекторной характеристики является малый коэффициент передачи, затрудняющий работу последующих усилительных каскадов.
В режиме «сильных» сигналов вольт-амперная характеристика диода аппроксимируется линейной зависимостью ig = f (Ug) (5.5). В этом случае появляется заметное напряжение смещения на аноде диода из-за значительной величины U =, т. е. диод работает в режиме отсечки, и ток проходит через него только в течение тех интервалов времени, когда Полагая, что u c(t) = U ccosωc t, ток открытого диода можно определить по выражению
где Интегрируя выражение (5.12) на интервале [0…2p], можно получить выражение для U = в виде
Учитывая, что
т. е. угол отсечки определяется лишь значениями S и R ни не зависит от величины U c. Для амплитудно-модулированного сигнала имеем u вых(t) = cosq U c[1 + m a x (t)] = U ccosq + m a U c x (t)cosq, (5.15) т. е., несмотря на наличие угла отсечки, диодный детектор и в режиме «сильных» сигналов является линейным детектором. Нелинейные искажения при детектировании «сильных» сигналов определяются: 1. Нелинейностью начального участка вольт-амперной характеристики диода. При этом, чтобы гарантировать работу вне существенно нелинейного участка, например, в области 0 ≤ U c ≤ U c(1) на рис. 5.2, необходимо выбирать значение U cисходя из неравенства
2. Различием сопротивлений детектора по постоянному и переменному токам. При использовании усилителя с входным сопротивлением R УНЧ ³ (5–10) R ни выборе величины емкости разделительного конденсатора C p, обеспечивающей его малое сопротивление по переменному току по сравнению с R УНЧ, из условия
где Ωmin – минимальная частота модулирующего сигнала, этим видом нелинейных искажений можно пренебречь. 3. Нелинейностью процесса заряда и разряда конденсатора C н. При этом возникает фазовый сдвиг между напряжениями U = и u a(t). В моменты времени, когда u a(t) < U =, конденсатор C нбудет разряжаться через резистор R нпо экспоненциальному закону. Анализ показывает, что малый уровень нелинейных искажений этого вида обеспечивается при условии
где Ωmax – максимальная частота модулирующего сигнала. Кроме рассмотренных выше нелинейных искажений в режиме детектирования «сильных» сигналов возникают частотные искажения, обусловленные присутствием в выходном напряжении гармоник высокочастотного колебания. С целью уменьшения уровня колебания высокой частоты на выходе амплитудного детектора величина емкости конденсатора C нвыбирается из условия
а коэффициент фильтрации в этом случае определяется выражением k ф = ωc C н rg, (5.20) где rg – сопротивление диода в открытом состоянии.
|

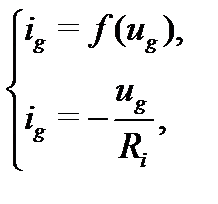 (5.5)
(5.5)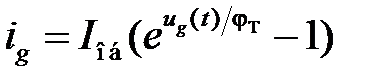 , (5.6)
, (5.6)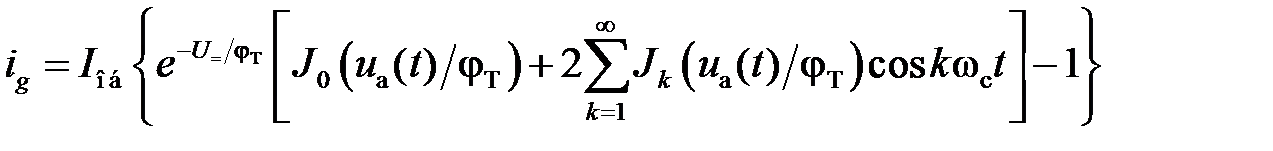 . (5.7)
. (5.7)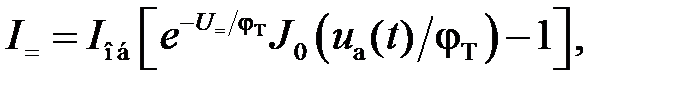
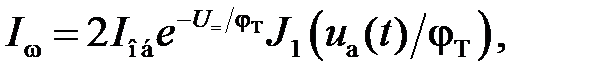 (5.8)
(5.8)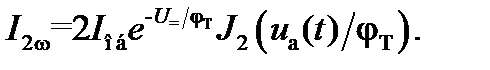
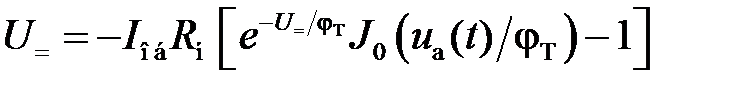 . (5.9)
. (5.9)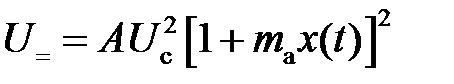 , (5.10)
, (5.10)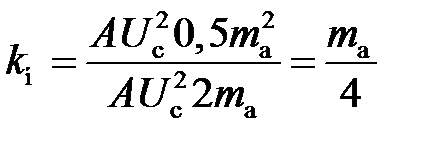 . (5.11)
. (5.11)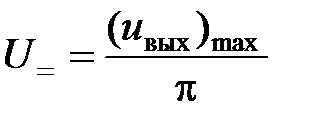
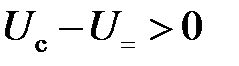 . На рис. 5.4 показан угол отсечки θтока диода. На интервале времени, соответствующем углу 2θ, происходит быстрый заряд конденсатора C н (см. рис. 5.1) через открытый диод. В течение времени, когда диод закрыт, конденсатор C н разряжается через резистор R н.
. На рис. 5.4 показан угол отсечки θтока диода. На интервале времени, соответствующем углу 2θ, происходит быстрый заряд конденсатора C н (см. рис. 5.1) через открытый диод. В течение времени, когда диод закрыт, конденсатор C н разряжается через резистор R н.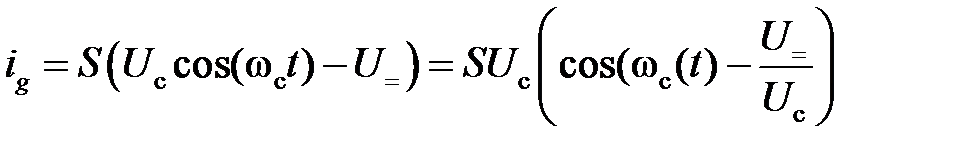 , (5.12)
, (5.12)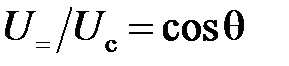 – косинус угла отсечки, S – крутизна вольт-амперной характеристики на рабочем участке.
– косинус угла отсечки, S – крутизна вольт-амперной характеристики на рабочем участке.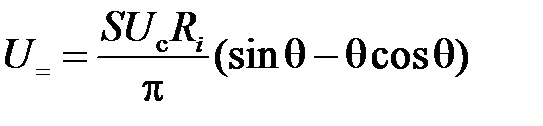 . (5.13)
. (5.13)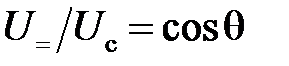 , для малых значений угла q получаем
, для малых значений угла q получаем , (5.14)
, (5.14) . (5.16)
. (5.16)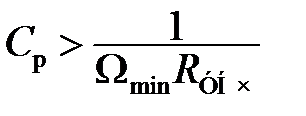 , (5.17)
, (5.17)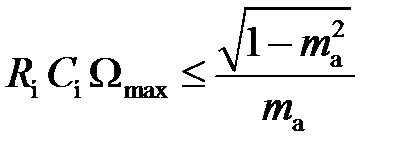 , (5.18)
, (5.18)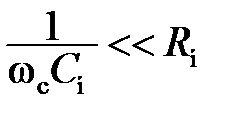 , (5.19)
, (5.19)


