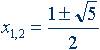Золотое сечение – гармоническая пропорция

В математике пропорцией (лат. proportio) называют равенство двух отношений: a: b= c: d.

Отрезок прямой АВ можно разделить на две части следующими способами:

- на две равные части – АВ: АС= АВ: ВС;

- на две неравные части в любом отношении (такие части пропорции не образуют);

таким образом, когда АВ: АС= АС: ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a: b= b: c или с: b= b: а.

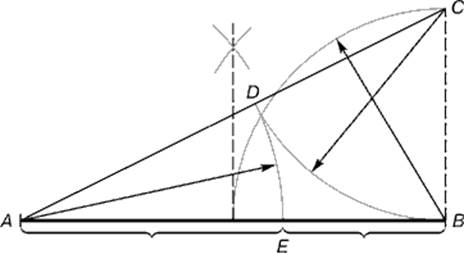
Рис.1.Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

 

Рис. 2. Деление отрезка прямой по золотому сечению. BC= 1/2 AB; CD= BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x2 – x – 1= 0

Решение этого уравнения:

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.