Двоичные сумматоры
Двоичными сумматорами называют логические устройства, выполняющие операцию сложения двух чисел, представленных в двоичном коде. В зависимости от способа обработки чисел различают последовательные и параллельные сумматоры. Параллельные сумматоры комбинационного типа представляют собой композиции одноразрядных суммирующих схем, причем обработка чисел в таких устройствах осуществляется одновременно во всех разрядах. В цифровых устройствах применяются одноразрядные суммирующие схемы на два и три входа, причем первую называют полусумматором, вторую - полным одноразрядным сумматором. Рассмотрим полусумматор, имеющий два входа а и b. Выходными сигналами такого устройства являются сумма S и перенос Р, которые вырабатываются согласно таблице функционирования данного устройства(рис. 2.12).
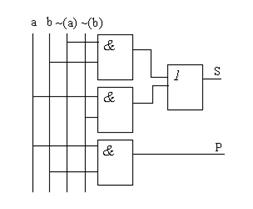
Рис. 2.12. Таблица истинности полусумматора Из таблицы следует, что полусумматор описывается двумя переключательными функциями: S = ~ (a)*b + a*~ (b), P = a*b, (1) Либо S = ~ (~ (a) ~ (b) + a*b), P = a*b, (2). Его реализация на основании соотношений (1) либо (2) требует наличия, во-первых, логических элементов И, ИЛИ, НЕ, во-вторых, прямых a, b и инверсных а, b кодов слагаемых (см. рис. 2.13).
Рис. 2.13. Полусумматор При синтезе комбинационных устройств (КУ) с несколькими выходами целесообразно логические функции преобразовать так, чтобы одно и то же логическое выражение в разных формулах использовалось несколько раз. Это позволит сократить общее количество логических элементов, необходимых для построения КУ. В результате преобразования получим S = a*(not(P)) + b*(not(P)), P = a*b. Сумматор в отличие от полусумматора должен воспринимать не два, а три входных сигнала: два слагаемых a, b и сигнал переноса с предыдущего разряда P. Составим таблицу функционирования полного одноразрядного сумматора (табл. 2). Таблица 2
Из таблицы следует S = ~(a)*~ (b)*p + ~ (a)*b*~ (p) + a*~ (b)*~ (p) + a*b*p, (4) P = ~ (a)*b*p + a*~ (b)*p + a*b*~ (p) + a*b*p.
|