Согласно представлениям классической физики электроны в атоме движутся по замкнутым траекториям – орбитам, образуя систему замкнутых орбитальных токов. Если электрон движется со скоростью  по круговой орбите радиуса r (рис. 1), то сила орбитального тока
по круговой орбите радиуса r (рис. 1), то сила орбитального тока  будет равна:
будет равна:
 (2)
(2)
где e=1,6*10-19Кл – заряд электрона. Поскольку электрон имеет отрицательный заряд, то направление орбитального тока  обратно направлению скорости движения электрона. Такой круговой виток с током создает магнитное поле, характеризующееся магнитным моментом
обратно направлению скорости движения электрона. Такой круговой виток с током создает магнитное поле, характеризующееся магнитным моментом 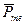 , величина которого:
, величина которого:
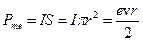 (3)
(3)
Кроме того, каждый электрон имеет собственный магнитный момент 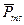 , называемый «магнитным спином», являющийся неотъемлемой характеристикой электрона. Наличие спинового магнитного момента
, называемый «магнитным спином», являющийся неотъемлемой характеристикой электрона. Наличие спинового магнитного момента 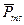 у электрона не может быть объяснено с позиций классической физики, но оно было доказано экспериментально и легло в основу квантовой теории строения атома.
у электрона не может быть объяснено с позиций классической физики, но оно было доказано экспериментально и легло в основу квантовой теории строения атома.
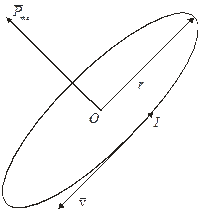
рис. 1
Атом (или молекула) вещества, содержащий несколько электронов будет иметь магнитный момент 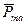 , равный:
, равный:
 (4)
(4)
где N – число электронов в атоме.
Если магнетик поместить во внешнее магнитное поле с индукцией  , то каждый атом (молекула) этого вещества реагирует на появление
, то каждый атом (молекула) этого вещества реагирует на появление  двояким образом:
двояким образом:
1. На атом начинает действовать момент силы 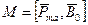 , стремящийся повернуть атом так, чтобы направления векторов
, стремящийся повернуть атом так, чтобы направления векторов 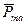 и
и  совпадали (рис. 2). Это приводит к тому, что возникает внутреннее магнитное поле
совпадали (рис. 2). Это приводит к тому, что возникает внутреннее магнитное поле 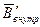 , и оно усиливает индукцию
, и оно усиливает индукцию  магнитного поля в веществе.
магнитного поля в веществе.
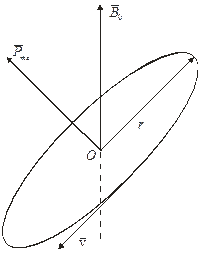
рис. 2
2. Орбита каждого электрона начинает прецессировать вокруг направления вектора  (рис. 3) со скоростью
(рис. 3) со скоростью  , создавая направленный орбитальный магнитный момент
, создавая направленный орбитальный магнитный момент 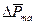 , направление которого противоположно направлению вектора
, направление которого противоположно направлению вектора  . Это приводит к тому, что возникает внутреннее магнитное поле
. Это приводит к тому, что возникает внутреннее магнитное поле 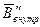 , направленное противоположно
, направленное противоположно  и ослабляющее магнитное поле в веществе.
и ослабляющее магнитное поле в веществе.

рис. 3
Эти два конкурирующих процесса и определяют величину результирующей магнитной индукции 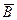 в веществе. У диамагнетиков
в веществе. У диамагнетиков 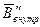 >
> 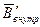 и
и 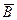 <
<  .
.
К диамагнетикам, как правило, относятся вещества, у которых в отсутствие внешнего магнитного поля полный магнитный момент атома (молекулы) 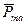 равен нулю (висмут, золото, сурьма, графит, цинк и др.). К парамагнетикам относятся вещества, у которых полный магнитный момент атома
равен нулю (висмут, золото, сурьма, графит, цинк и др.). К парамагнетикам относятся вещества, у которых полный магнитный момент атома 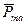 не равен нулю (алюминий, платина, щелочные металлы и др.). У таких веществ
не равен нулю (алюминий, платина, щелочные металлы и др.). У таких веществ 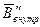 <
< 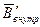 и
и 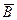 >
>  .
.
Количественной характеристикой намагниченного состояния вещества служит векторная величина  , называемая намагниченностью, равная отношению магнитного момента
, называемая намагниченностью, равная отношению магнитного момента 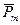 макроскопически малого объема вещества
макроскопически малого объема вещества  к этому объему:
к этому объему:
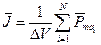 (5)
(5)
где 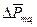 – магнитный момент i – ого атома (молекулы) из общего числа N атомов (молекул), содержащихся в объеме
– магнитный момент i – ого атома (молекулы) из общего числа N атомов (молекул), содержащихся в объеме  . Этот объем
. Этот объем  должен быть малым, чтобы в его пределах магнитное поле можно было считать однородным, но содержать большое количество атомов (N>>1), чтобы к ним можно было применять статистические методы. Намагниченность вещества
должен быть малым, чтобы в его пределах магнитное поле можно было считать однородным, но содержать большое количество атомов (N>>1), чтобы к ним можно было применять статистические методы. Намагниченность вещества  зависит от напряженности магнитного поля
зависит от напряженности магнитного поля 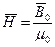 (рис. 4). При небольших значениях
(рис. 4). При небольших значениях  зависимость
зависимость 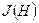 почти линейная, но при дальнейшем увеличении
почти линейная, но при дальнейшем увеличении  характер этой зависимости изменяется и наступает насыщение (
характер этой зависимости изменяется и наступает насыщение (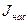 на Рис. 4).
на Рис. 4).
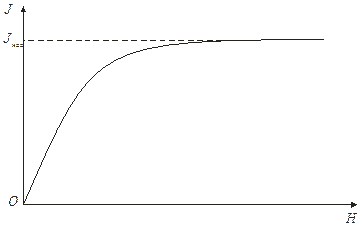
рис. 4
Такой характер зависимости 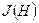 физически можно объяснить следующим образом: при увеличении
физически можно объяснить следующим образом: при увеличении  все большее число молекул выстраивается так, чтобы их магнитные моменты
все большее число молекул выстраивается так, чтобы их магнитные моменты 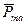 были ориентированы по направлению внешнего магнитного поля (линейный участок кривой
были ориентированы по направлению внешнего магнитного поля (линейный участок кривой 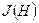 ). Однако, когда большая часть молекул будет уже сориентирована, то наступает насыщение и увеличение
). Однако, когда большая часть молекул будет уже сориентирована, то наступает насыщение и увеличение  уже не влияет на
уже не влияет на  .
.
Зависимость 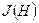 на линейном участке можно выразить формулой:
на линейном участке можно выразить формулой:
 (6)
(6)
где 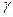 – магнитная восприимчивость вещества. Результирующая индукция магнитного поля в веществе будет тогда равна:
– магнитная восприимчивость вещества. Результирующая индукция магнитного поля в веществе будет тогда равна:
 (7)
(7)
Здесь 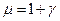 – магнитная проницаемость вещества. Величина
– магнитная проницаемость вещества. Величина 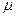 показывает, во сколько раз индукция магнитного поля
показывает, во сколько раз индукция магнитного поля 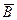 в данном веществе будет больше индукции
в данном веществе будет больше индукции 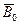 магнитного поля в вакууме. Для парамагнетиков
магнитного поля в вакууме. Для парамагнетиков 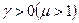 и ее величина
и ее величина 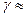 10-2–10-4, для диамагнетиков
10-2–10-4, для диамагнетиков  и ее величина
и ее величина 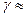 10-3–10-5. Парамагнетики и диамагнетики являются слабомагнитными веществами и во многих расчетах можно принимать для них
10-3–10-5. Парамагнетики и диамагнетики являются слабомагнитными веществами и во многих расчетах можно принимать для них 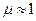 .
.

 по круговой орбите радиуса r (рис. 1), то сила орбитального тока
по круговой орбите радиуса r (рис. 1), то сила орбитального тока  будет равна:
будет равна: (2)
(2)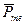 , величина которого:
, величина которого: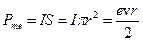 (3)
(3)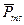 , называемый «магнитным спином», являющийся неотъемлемой характеристикой электрона. Наличие спинового магнитного момента
, называемый «магнитным спином», являющийся неотъемлемой характеристикой электрона. Наличие спинового магнитного момента 
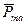 , равный:
, равный: (4)
(4) , то каждый атом (молекула) этого вещества реагирует на появление
, то каждый атом (молекула) этого вещества реагирует на появление 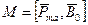 , стремящийся повернуть атом так, чтобы направления векторов
, стремящийся повернуть атом так, чтобы направления векторов 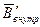 , и оно усиливает индукцию
, и оно усиливает индукцию 
 , создавая направленный орбитальный магнитный момент
, создавая направленный орбитальный магнитный момент 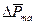 , направление которого противоположно направлению вектора
, направление которого противоположно направлению вектора 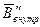 , направленное противоположно
, направленное противоположно 
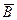 в веществе. У диамагнетиков
в веществе. У диамагнетиков  , называемая намагниченностью, равная отношению магнитного момента
, называемая намагниченностью, равная отношению магнитного момента 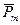 макроскопически малого объема вещества
макроскопически малого объема вещества  к этому объему:
к этому объему: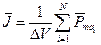 (5)
(5)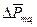 – магнитный момент i – ого атома (молекулы) из общего числа N атомов (молекул), содержащихся в объеме
– магнитный момент i – ого атома (молекулы) из общего числа N атомов (молекул), содержащихся в объеме 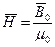 (рис. 4). При небольших значениях
(рис. 4). При небольших значениях  зависимость
зависимость 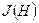 почти линейная, но при дальнейшем увеличении
почти линейная, но при дальнейшем увеличении 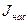 на Рис. 4).
на Рис. 4).
 (6)
(6)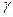 – магнитная восприимчивость вещества. Результирующая индукция магнитного поля в веществе будет тогда равна:
– магнитная восприимчивость вещества. Результирующая индукция магнитного поля в веществе будет тогда равна: (7)
(7)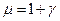 – магнитная проницаемость вещества. Величина
– магнитная проницаемость вещества. Величина 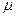 показывает, во сколько раз индукция магнитного поля
показывает, во сколько раз индукция магнитного поля 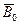 магнитного поля в вакууме. Для парамагнетиков
магнитного поля в вакууме. Для парамагнетиков 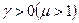 и ее величина
и ее величина 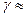 10-2–10-4, для диамагнетиков
10-2–10-4, для диамагнетиков  и ее величина
и ее величина 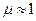 .
.


