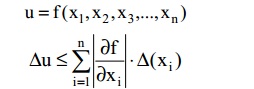Погрешность вычислений. Погрешность функции.
I. ТЕОРИЯ ПОГРЕШНОСТЕЙ Основная задача теории погрешностей состоит в оценке погрешности результата вычислений при известных погрешностях исходных данных. Абсолютная и относительная погрешности. Пусть α* – точное (и никогда неизвестное) значение некоторой величины, nа α – приближенное значение этой же величины. Абсолютной погрешностью приближенного значения α называется вели- чина: ∆(a)=abs(a-a*) Относительной погрешностью приближенного значения α называется величина: δ(α)= abs(a-a*)/abs(a) Особенности машинной арифметики Вещественные числа в ЭВМ представляются в экспоненциальном виде (с плавающей точкой): D= +- m * 10^(+-n), где m - мантисса и n – порядок. Пример записи: 5 = 0.05*10^2 Погрешность вычислений. Погрешность функции. Погрешности вычислений. 1. Абсолютная погрешность суммы или разности нескольких чисел не пре- восходит суммы абсолютных погрешностей этих чисел. 2. Относительная погрешность суммы: δ(а+b) <= δmax 3.Относительная погрешность разности: δ(a-b)<= v* δmax, где v=abs(a+b)/abs(a-b) 4. Относительные погрешности произведения и частного: δ(a*b)= δ(a/b)= δ(a)+ δ(b). 5. Абсолютная погрешность дифференцируемой функции многих перемен- ных:
|