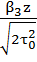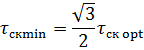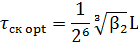Эффекты дисперсии высших порядков
1. Третье и высшие приближения теории 2. Фурье-оптика волновых пакетов 3. Распространение фазово-модулированных импульсов. Понятие о аберрации 1. В тех случаях, когда параметр β(ω) = где
Будем рассматривать уравнение распространения в предположении того, что все иные эффекты отсутствуют, а остаются лишь те, которые связаны с проявлением дисперсии в системе. Уравнение будет иметь вид: ( Решение данного уравнения: A (t, z) =
Нахождение A (t, z) может быть осуществлено приближенно. В общем случае уравнение решается численными методами и его решение можно представить качественно, основываясь на двух параметрах:
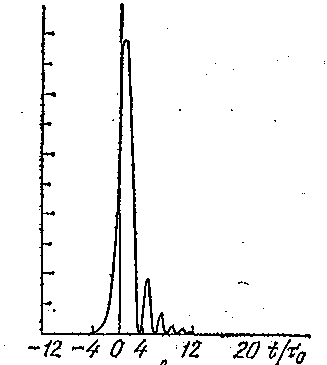
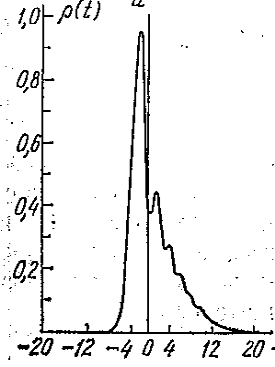
а б
в г а – гауссовский импульс на входе б – в – г – Отсюда следует, что кубическая дисперсия ведет к качественному новому поведению системы. Если работает только дисперсия второго порядка (б), в системе наблюдается обычное симметричное уширение импульса. Если действует дисперсия только третьего порядка, всё зависит от ее знака. Если Определим фурье-спектр интенсивности как: Н(х) = Тогда можно ввести понятие функции интенсивности импульса в диспергирующей среде следующей формулой: I (t, z) = С помощью данной интенсивности можно ввести среднюю квадратичную длительность После преобразования
В общем виде длительность среднеквадратичного импульса:
В дальней зоне τ ≈ Можно ввести минимальную среднеквадратичную длительность
Учет эффектов высшего порядка только уточняет картину, полученную во втором и третьем приближении. При распространении в таких сложных условиях исходят из теоремы площадей: в среде без потерь (𝛼 = 0) независимо от проявляемых дисперсионных нелинейных эффектов, площадь под огибающей импульса должна оставаться постоянной величиной. 2. Фурье-оптика основывается на теории дифракции Фраунгофера: спектр поля в дальней зоне определяется преобразованием Фурье от распределения комплексной амплитуды на входе. Аббе было предложено влиять на изображение с помощью изменения амплитуд и фаз спектральных компонент в фокальной плоскости. Классические примеры этой техники – метод темного поля и метод фазового контраста. На аналогичных преобразованиях световых импульсов, происходящих в диспергирующих средах, основана фурье-оптика волновых пакетов. Здесь особый интерес представляют новые методы преобразования коротких импульсов в искусственных диспергирующих средах. Сильно диспергирующие системы, представляющие собой комбинации дифракционных решеток и призм, позволяют развернуть частотный фурье-спектр в пространстве и управлять амплитудами и фазами компонент частотного спектра – совершенно аналогично тому, как это делал Аббе с фурье-компонентами углового спектра.
|

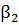 →0, т.е. система находится в точке нулевой дисперсии, тогда необходимо изучать высшие порядки разложения постоянной распространения в ряд (по частоте пробного поля), т.е. речь идет о параметре
→0, т.е. система находится в точке нулевой дисперсии, тогда необходимо изучать высшие порядки разложения постоянной распространения в ряд (по частоте пробного поля), т.е. речь идет о параметре  и др. Постоянная распространения представляется в форме следующего разложения:
и др. Постоянная распространения представляется в форме следующего разложения: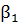 (ω –
(ω – 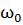 ) +
) + 
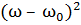 +
+ 
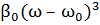 + …,
+ …,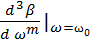

 –
– 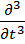 )A (t, z) = 0
)A (t, z) = 0 , где
, где – ядро интеграла, выраженное функцией Грина, которая имеет вид
– ядро интеграла, выраженное функцией Грина, которая имеет вид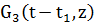 =
= 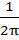
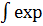 (-i [
(-i [ 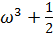
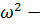 (
(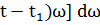
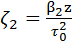 ,
, 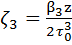

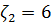 ,
, 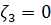
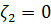 ,
, 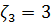
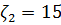 ,
, 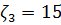
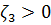 , происходит глубокая модуляция хвоста импульса, фронт остается гладким. Если
, происходит глубокая модуляция хвоста импульса, фронт остается гладким. Если  , наоборот, модулируется фронт, импульс в среде становится асимметричным, его центр тяжести смещается (в). Наложение дисперсии второго и третьего порядка друг на друга приводит к одновременному уширению и модуляции фронтов импульса (г).
, наоборот, модулируется фронт, импульс в среде становится асимметричным, его центр тяжести смещается (в). Наложение дисперсии второго и третьего порядка друг на друга приводит к одновременному уширению и модуляции фронтов импульса (г).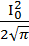
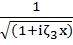 exp (-i
exp (-i 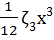 –
– 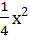 –
– 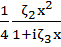 )
) =
=  dx.
dx. =
= 
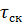 =
= 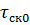
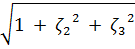 , где
, где  , где
, где =
= 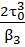
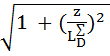
 =
= 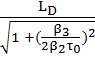
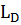 – дисперсионная длина второго порядка
– дисперсионная длина второго порядка