51.Арифметические приложения теории сравнений. Вычисление остатков при делении на данное число.
Под системой счисления понимают «совокупность приемов обозначения (записи) чисел. позиционные системы счисления. Это такие системы счисления, в которых значение любой цифры числа определяется не только ее очертанием, но и положением. Количество различных цифр, используемых в позиционной системе счисления для изображения любого числа, называют основанием системы счисления. Различают позиционные и непозиционные системы счисления.Все позиционные системы объединяет общий принцип построения. Пусть 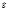 - основание системы счисления, тогда записать число в
- основание системы счисления, тогда записать число в 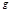 -чной системе счисления это значит представить его либо в цифровой форме:
-чной системе счисления это значит представить его либо в цифровой форме:  , либо в многочленной форме:
, либо в многочленной форме:  (если число
(если число  - целое, то
- целое, то  ),где
),где 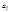 – цифра системы счисления. Основание системы счисления в начальный период утверждения таких систем счисления истолковывалось как отношение единиц двух любых соседних разрядов в числе: каждая единица следующего разряда в «
– цифра системы счисления. Основание системы счисления в начальный период утверждения таких систем счисления истолковывалось как отношение единиц двух любых соседних разрядов в числе: каждая единица следующего разряда в «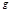 » раз больше единицы предшествующего разряда. Со временем, однако, такое толкование понятия «основание системы счисления» расширилось. Сегодня существуют так называемые обобщенные системы счисления.
» раз больше единицы предшествующего разряда. Со временем, однако, такое толкование понятия «основание системы счисления» расширилось. Сегодня существуют так называемые обобщенные системы счисления.
Систематической записью натурального числа 
 по основанию
по основанию  называется его представление в виде
называется его представление в виде  , где
, где 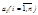 - цифры числа, причем
- цифры числа, причем  и
и  <
< 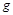 . Теорема. Всякое натуральное число
. Теорема. Всякое натуральное число  может быть единственным образом представлено в виде систематической записи по любому основанию
может быть единственным образом представлено в виде систематической записи по любому основанию  >1.
>1.
Способ замены данного числа  другим числом, чтобы вычисления остатка от деления на
другим числом, чтобы вычисления остатка от деления на  значительно упростилось был предложен французским математиком Б. Паскалем (1623-1662).
значительно упростилось был предложен французским математиком Б. Паскалем (1623-1662).
Пусть 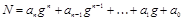 .Обозначим абсолютно наименьший вычет числа
.Обозначим абсолютно наименьший вычет числа  по модулю
по модулю  через
через 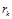 , так что
, так что 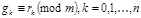 .
.
Тогда 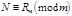 , где
, где 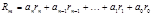 .Отсюда следует, что число
.Отсюда следует, что число  при делении на
при делении на 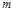 даёт такой же остаток, как и
даёт такой же остаток, как и 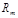 .
.





 52.Систематические числа, установление признаков делимости чисел.
52.Систематические числа, установление признаков делимости чисел.
Рассмотренный выше способ отыскания остатков при делении чисел может быть использован при выводе признаков делимости, так как число  делится на
делится на  , когда
, когда 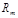 делится на
делится на  .
.
Замечание. Рассмотренный в предыдущем пункте пример позволяет сформулировать аналогичный признак делимости на 8 в 10-чной системе счисления: число в 10-чной системе счисления делится на 8, если делится на 8 число, составленное из последних трёх цифр исходного числа.
Как видим, ряд признаков делимости, причём даже для различных систем счисления, имеют похожую формулировку. Сформулируем ряд более общих признаков делимости.
Теорема1. Пусть 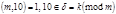 и число
и число  записано в виде (2) в десятичной системе счисления. Число
записано в виде (2) в десятичной системе счисления. Число  делится на
делится на 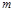 тогда и только тогда, когда на
тогда и только тогда, когда на  делится сумма чисел, которые получаются при разбиении справа налево цифровой записи числа
делится сумма чисел, которые получаются при разбиении справа налево цифровой записи числа  на грани по
на грани по  цифр в каждой грани.
цифр в каждой грани.
Доказательство.
Запишем число  в системе счисления с основанием
в системе счисления с основанием 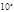 :
: 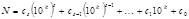
где  для всех
для всех 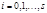 .
.
Из (3) видно, что 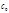 - остаток от деления
- остаток от деления  на
на  , т.е.
, т.е.  - число, которое в десятичной системе счисления имеет цифры одинаковые с последними
- число, которое в десятичной системе счисления имеет цифры одинаковые с последними  цифрами числа
цифрами числа  .
.
Далее получаем, что 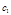 - остаток от деления числа
- остаток от деления числа  на
на 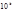 , т.е.
, т.е.  - число, которое в 10-чной системе счисления имеет цифры такие же, как в предпоследней грани из
- число, которое в 10-чной системе счисления имеет цифры такие же, как в предпоследней грани из  чисел у числа
чисел у числа  , и т.д.Таким образом,
, и т.д.Таким образом,  - числа, которые получаются при разбиении справа налево числа
- числа, которые получаются при разбиении справа налево числа  на грани по
на грани по  цифр в каждой грани. Так как
цифр в каждой грани. Так как 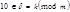 , то
, то 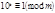 , тогда
, тогда 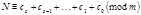 . Следовательно, число
. Следовательно, число 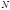 делится на
делится на 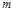 тогда и только тогда, когда на
тогда и только тогда, когда на  делится сумма чисел, которые получаются при разбиении справа налево числа
делится сумма чисел, которые получаются при разбиении справа налево числа  на грани по
на грани по  цифр.
цифр.
Замечание. Сформулированные признак делимости на 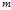 всегда будет таков, что количество цифр в каждой грани не больше
всегда будет таков, что количество цифр в каждой грани не больше 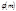 . Наименее удобен этот признак, когда
. Наименее удобен этот признак, когда  максимальное. Например, так как 10 первообразный корень по
максимальное. Например, так как 10 первообразный корень по 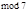 , т.е.
, т.е. 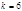 , то число для проверки делимости на 7 придётся разбивать на грани по 6 цифр. Очевидно, что применять такой признак имеет смысл, если исследуемое число очень велико
, то число для проверки делимости на 7 придётся разбивать на грани по 6 цифр. Очевидно, что применять такой признак имеет смысл, если исследуемое число очень велико
Рассмотрим признак делимости на  и
и 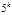 .
.
Теорема 2. Пусть 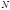 записано в десятичной системе счисления в виде (2). Число
записано в десятичной системе счисления в виде (2). Число  делится на
делится на 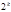 (на
(на  ) тогда и только тогда, когда на
) тогда и только тогда, когда на 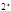 (на
(на  ) делится на число, имеющее те же цифры, что и последние
) делится на число, имеющее те же цифры, что и последние 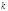 цифр числа
цифр числа 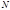 .
.
Доказательство.
Пусть  , где
, где  , т.е.
, т.е.  - число, имеющее те же цифры, что и последние
- число, имеющее те же цифры, что и последние  цифр числа
цифр числа  .
.
Если 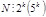 , то и
, то и 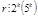 .
.
Обобщением выведенного выше признака делимости на 11 является
Теорема 3. Пусть 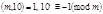 и
и  записано в десятичной системе счисления. Число
записано в десятичной системе счисления. Число 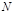 делится на
делится на 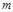 тогда и только тогда, когда на
тогда и только тогда, когда на 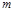 делится сумма взятых попеременно со знаком плюс и минус чисел, которые получаются при разбиении справа налево цифровой записи числа
делится сумма взятых попеременно со знаком плюс и минус чисел, которые получаются при разбиении справа налево цифровой записи числа 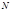 на грани по
на грани по  цифр в каждой грани. Например, так как
цифр в каждой грани. Например, так как 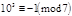 , то число делится на 7, если на 7 делится сумма взятых попеременно со знаком «плюс» и «минус» чисел, получающихся при разбиении справа налево числа
, то число делится на 7, если на 7 делится сумма взятых попеременно со знаком «плюс» и «минус» чисел, получающихся при разбиении справа налево числа 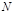 на грани по 3 цифры.
на грани по 3 цифры.
Замечание. Приведённые теоремы можно сформулировать для системы счисления с любым основанием  .
.
53.Определение длины периода, получающегося при обращении обыкновенной дроби в g-чную.
Применим свойства сравнения для определения длины периода, получающегося при обобщении обыкновенной дроби  в
в 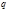 - чную. Предварительно выведем формулу для нахождения цифры числа.Пусть
- чную. Предварительно выведем формулу для нахождения цифры числа.Пусть 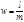 ,
, 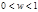 . Запишем это число в
. Запишем это число в 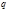 - чной системе счисления:
- чной системе счисления:
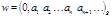 , (4)
, (4)
где 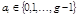 .
.
Найдём формулу для вычисления цифры  . Умножим (4) на
. Умножим (4) на  :
: 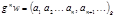 (5)
(5)
Возьмем целую часть от обеих частей равенства (5): 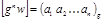 (6)
(6)
Аналогично
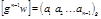 (7)
(7)
Умножим (7) на  :
:
 (8)
(8)
Вычитая из (6) равенство (8), получаем формулу для вычисления цифры  , стоящей на
, стоящей на  - м месте после запятой в числе
- м месте после запятой в числе 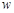
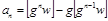 . (9)
. (9)
Теорема (о длине периода 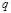 - чной дроби). Если
- чной дроби). Если 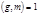 , то длина периода получающегося при обращении рационального числа
, то длина периода получающегося при обращении рационального числа  в
в 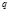 - чную дробь равна показателю
- чную дробь равна показателю  числа
числа  по
по  .
.
Доказательство.
Для доказательства теоремы покажем, что цифра стоящая на  месте равна цифре на
месте равна цифре на  -м месте.
-м месте.
По формуле (9)  .
.
Так как 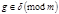 , то
, то  - наименьшее число, для которого
- наименьшее число, для которого  ,т. е.
,т. е. 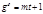 , где
, где 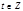 .
.
Тогда

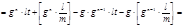
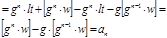 .
.
Так как 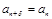 , то цифры числа
, то цифры числа  повторяются через
повторяются через 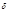 цифр.
цифр.
Замечание1. Период при обращении обыкновенной дроби в систематическую зависит только от знаменателя дроби, т.е. все дроби имеющие одинаковый знаменатель имеют одинаковую длину периода при обращении в систематическую дробь.
Замечание 2. Наибольшую длину периода имеют дроби 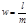 , для которых основание системы
, для которых основание системы  - первообразный корень по
- первообразный корень по  .
.
54. Проверка результатов арифметических действий
Теория сравнения даёт удобный способ проверки правильности арифметических действии. Пусть при сложении получено 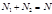 и
и 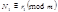 ,
, 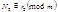 ,
, 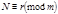 .
.
Если сложение выполнено правильно, то  .
.
Аналогично, из правильности соотношений  следует
следует 
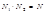 следует
следует 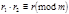 .
.
Замечание. Для проверки соотношения 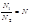 представляем его в виде
представляем его в виде 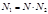 . Таким образом, при проверке большие числа заменяют на небольшие, сравнимые с ними по модулю. Применение этого способа проверки имеет смыл только тогда, когда нахождение остатков
. Таким образом, при проверке большие числа заменяют на небольшие, сравнимые с ними по модулю. Применение этого способа проверки имеет смыл только тогда, когда нахождение остатков  по
по  осуществляется легко и быстро. Поэтому в качестве модуля
осуществляется легко и быстро. Поэтому в качестве модуля 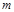 выбирают число
выбирают число  или (и)
или (и) 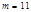 .
.
Способ «Проверки с помощью девятки». Каждое число, записанное в десятичной системе счисления, сравнимо с суммой его цифр по модулю 9. Для каждого числа вычисляют остаток от деления на 9 суммы цифр. Производя действия на числами, производят такие же действия над этими остатками. Результат рассматриваемых действий над этими остатками должен отличаться от суммы цифр искомого результата на число кратное 9. Если ошибка кратна 9, то она замечена не будет.
Способ «Проверки с помощью одиннадцати». По модулю 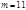 каждое число, записанное в десятичной системе счисления, будет сравнимо с разностью суммы цифр, стоящих на нечётном месте, и суммы цифр, стоящих на нечётном месте. Для каждого числа вычисляют остаток от деления на 11 разности между суммами цифр, стоящих на чётном и нечётном местах. Результат рассматриваемых действий над этими остатками должен отличаться от разности сумм цифр на чётном и нечётном местах искомого результат на число кратное 11. Если ошибка кратна 11, то она не будет обнаружена.
каждое число, записанное в десятичной системе счисления, будет сравнимо с разностью суммы цифр, стоящих на нечётном месте, и суммы цифр, стоящих на нечётном месте. Для каждого числа вычисляют остаток от деления на 11 разности между суммами цифр, стоящих на чётном и нечётном местах. Результат рассматриваемых действий над этими остатками должен отличаться от разности сумм цифр на чётном и нечётном местах искомого результат на число кратное 11. Если ошибка кратна 11, то она не будет обнаружена.
Замечание. При сложных вычислениях имеет смысл производить две проверки с помощью 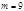 и с помощью
и с помощью 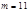 . Тогда необнаруженными могут быть только ошибки кратные 99.
. Тогда необнаруженными могут быть только ошибки кратные 99.

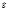 - основание системы счисления, тогда записать число в
- основание системы счисления, тогда записать число в 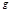 -чной системе счисления это значит представить его либо в цифровой форме:
-чной системе счисления это значит представить его либо в цифровой форме:  , либо в многочленной форме:
, либо в многочленной форме:  (если число
(если число  - целое, то
- целое, то  ),где
),где 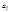 – цифра системы счисления. Основание системы счисления в начальный период утверждения таких систем счисления истолковывалось как отношение единиц двух любых соседних разрядов в числе: каждая единица следующего разряда в «
– цифра системы счисления. Основание системы счисления в начальный период утверждения таких систем счисления истолковывалось как отношение единиц двух любых соседних разрядов в числе: каждая единица следующего разряда в «
 по основанию
по основанию  называется его представление в виде
называется его представление в виде  , где
, где 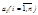 - цифры числа, причем
- цифры числа, причем  и
и  <
< 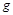 . Теорема. Всякое натуральное число
. Теорема. Всякое натуральное число  может быть единственным образом представлено в виде систематической записи по любому основанию
может быть единственным образом представлено в виде систематической записи по любому основанию  >1.
>1. значительно упростилось был предложен французским математиком Б. Паскалем (1623-1662).
значительно упростилось был предложен французским математиком Б. Паскалем (1623-1662).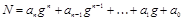 .Обозначим абсолютно наименьший вычет числа
.Обозначим абсолютно наименьший вычет числа  по модулю
по модулю 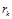 , так что
, так что 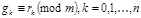 .
.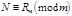 , где
, где 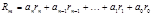 .Отсюда следует, что число
.Отсюда следует, что число 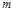 даёт такой же остаток, как и
даёт такой же остаток, как и 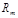 .
.

 52.Систематические числа, установление признаков делимости чисел.
52.Систематические числа, установление признаков делимости чисел. делится на
делится на  , когда
, когда  .
. 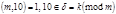 и число
и число  записано в виде (2) в десятичной системе счисления. Число
записано в виде (2) в десятичной системе счисления. Число 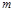 тогда и только тогда, когда на
тогда и только тогда, когда на  цифр в каждой грани.
цифр в каждой грани.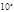 :
: 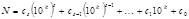
 для всех
для всех 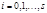 .
.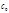 - остаток от деления
- остаток от деления  , т.е.
, т.е.  - число, которое в десятичной системе счисления имеет цифры одинаковые с последними
- число, которое в десятичной системе счисления имеет цифры одинаковые с последними  цифрами числа
цифрами числа 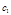 - остаток от деления числа
- остаток от деления числа  на
на 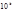 , т.е.
, т.е.  - число, которое в 10-чной системе счисления имеет цифры такие же, как в предпоследней грани из
- число, которое в 10-чной системе счисления имеет цифры такие же, как в предпоследней грани из  - числа, которые получаются при разбиении справа налево числа
- числа, которые получаются при разбиении справа налево числа 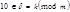 , то
, то 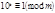 , тогда
, тогда 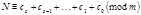 . Следовательно, число
. Следовательно, число 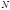 делится на
делится на  цифр.
цифр.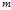 всегда будет таков, что количество цифр в каждой грани не больше
всегда будет таков, что количество цифр в каждой грани не больше 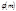 . Наименее удобен этот признак, когда
. Наименее удобен этот признак, когда  максимальное. Например, так как 10 первообразный корень по
максимальное. Например, так как 10 первообразный корень по 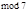 , т.е.
, т.е. 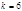 , то число для проверки делимости на 7 придётся разбивать на грани по 6 цифр. Очевидно, что применять такой признак имеет смысл, если исследуемое число очень велико
, то число для проверки делимости на 7 придётся разбивать на грани по 6 цифр. Очевидно, что применять такой признак имеет смысл, если исследуемое число очень велико и
и 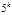 .
.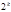 (на
(на  ) тогда и только тогда, когда на
) тогда и только тогда, когда на 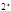 (на
(на 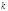 цифр числа
цифр числа 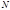 .
. , где
, где  , т.е.
, т.е.  - число, имеющее те же цифры, что и последние
- число, имеющее те же цифры, что и последние  цифр числа
цифр числа  .
.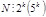 , то и
, то и 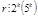 .
.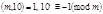 и
и 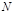 делится на
делится на 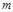 тогда и только тогда, когда на
тогда и только тогда, когда на 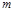 делится сумма взятых попеременно со знаком плюс и минус чисел, которые получаются при разбиении справа налево цифровой записи числа
делится сумма взятых попеременно со знаком плюс и минус чисел, которые получаются при разбиении справа налево цифровой записи числа 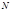 на грани по
на грани по  цифр в каждой грани. Например, так как
цифр в каждой грани. Например, так как 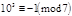 , то число делится на 7, если на 7 делится сумма взятых попеременно со знаком «плюс» и «минус» чисел, получающихся при разбиении справа налево числа
, то число делится на 7, если на 7 делится сумма взятых попеременно со знаком «плюс» и «минус» чисел, получающихся при разбиении справа налево числа  .
. в
в 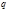 - чную. Предварительно выведем формулу для нахождения цифры числа.Пусть
- чную. Предварительно выведем формулу для нахождения цифры числа.Пусть 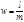 ,
, 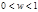 . Запишем это число в
. Запишем это число в 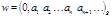 , (4)
, (4)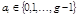 .
. . Умножим (4) на
. Умножим (4) на  :
: 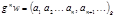 (5)
(5)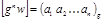 (6)
(6)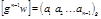 (7)
(7) :
: (8)
(8) , стоящей на
, стоящей на  - м месте после запятой в числе
- м месте после запятой в числе 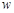
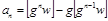 . (9)
. (9)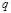 - чной дроби). Если
- чной дроби). Если 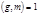 , то длина периода получающегося при обращении рационального числа
, то длина периода получающегося при обращении рационального числа  в
в 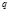 - чную дробь равна показателю
- чную дробь равна показателю  числа
числа  по
по  .
. месте равна цифре на
месте равна цифре на  -м месте.
-м месте. .
.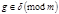 , то
, то  - наименьшее число, для которого
- наименьшее число, для которого  ,т. е.
,т. е. 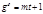 , где
, где 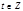 .
.
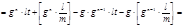
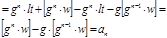 .
.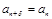 , то цифры числа
, то цифры числа  повторяются через
повторяются через 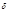 цифр.
цифр.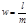 , для которых основание системы
, для которых основание системы  .
.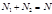 и
и 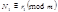 ,
, 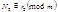 ,
, 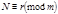 .
. .
. следует
следует 
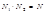 следует
следует 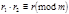 .
.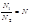 представляем его в виде
представляем его в виде 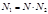 . Таким образом, при проверке большие числа заменяют на небольшие, сравнимые с ними по модулю. Применение этого способа проверки имеет смыл только тогда, когда нахождение остатков
. Таким образом, при проверке большие числа заменяют на небольшие, сравнимые с ними по модулю. Применение этого способа проверки имеет смыл только тогда, когда нахождение остатков  по
по 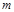 выбирают число
выбирают число  или (и)
или (и) 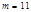 .
.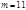 каждое число, записанное в десятичной системе счисления, будет сравнимо с разностью суммы цифр, стоящих на нечётном месте, и суммы цифр, стоящих на нечётном месте. Для каждого числа вычисляют остаток от деления на 11 разности между суммами цифр, стоящих на чётном и нечётном местах. Результат рассматриваемых действий над этими остатками должен отличаться от разности сумм цифр на чётном и нечётном местах искомого результат на число кратное 11. Если ошибка кратна 11, то она не будет обнаружена.
каждое число, записанное в десятичной системе счисления, будет сравнимо с разностью суммы цифр, стоящих на нечётном месте, и суммы цифр, стоящих на нечётном месте. Для каждого числа вычисляют остаток от деления на 11 разности между суммами цифр, стоящих на чётном и нечётном местах. Результат рассматриваемых действий над этими остатками должен отличаться от разности сумм цифр на чётном и нечётном местах искомого результат на число кратное 11. Если ошибка кратна 11, то она не будет обнаружена.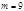 и с помощью
и с помощью 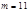 . Тогда необнаруженными могут быть только ошибки кратные 99.
. Тогда необнаруженными могут быть только ошибки кратные 99.


