Метод подбора заключается в использовании в качестве решений чисел полной системы вычетов. Заметим, что метод целесообразно применять, если модуль сравнения не очень большой. Для решения сравнения 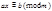 нужно:
нужно:
1. Выяснить количество решений сравнения (согласно доказанной выше теореме).
2. Если сравнение имеет  решений, то перейти к сравнению (5) и найти его решение
решений, то перейти к сравнению (5) и найти его решение 
3. Записать все решения исходного сравнения в виде (6). Решение сравнений первой степени методом подбора не является эффективным. На практике для небольших модулей m целесообразнее, используя свойства сравнений, преобразовать коэффициенты так, чтобы правую часть можно было бы разделить на коэффициент у неизвестного  Преобразованиям можно подвергать
Преобразованиям можно подвергать  или,
или,  а также
а также  и
и  сразу.
сразу.
Наиболее часто выполняют следующие преобразования:
- замена коэффициентов абсолютно наименьшими вычетами;
- прибавление к  числа, кратного модулю;
числа, кратного модулю;
- переход от  и
и  к сравнимым с ними числам, у которых есть общий делитель.
к сравнимым с ними числам, у которых есть общий делитель.
27.Применение теоремы Эйлера для решения сравнений первой степени.
Теорема. При  решением сравнения
решением сравнения  является класс
является класс  (7).
(7).
Доказательство.
Действительно, умножим обе части данного сравнения на 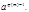

По теореме Эйлера  при
при 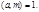 Поэтому получае
Поэтому получае 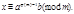
Замечание. Решением линейного сравнения по формуле (7) носит название метода Эйлера. 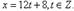
28.Применение цепных дробей для решения линейных сравнений
Теорема. Если 
 последовательность подходящихдробей разложения
последовательность подходящихдробей разложения 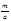 в цепную дробь и
в цепную дробь и 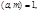 то решением сравнения
то решением сравнения  является класс
является класс 
Доказательство. Т.к. 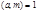 и, учитывая, что подходящие дроби несократимы, то из равенства
и, учитывая, что подходящие дроби несократимы, то из равенства  следует, что
следует, что  По свойству подходящих дробей
По свойству подходящих дробей  Тогда
Тогда  или
или  или
или 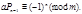 Умножим на
Умножим на  получим
получим  или
или 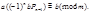 Отсюда следует, что число
Отсюда следует, что число  удовлетворяет данному сравнению, т.е.
удовлетворяет данному сравнению, т.е. 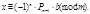
29.Неопределенные уравнения первой степени.
Определение. Диофантовым уравнением 1-ой степени с n неизвестными называется уравнение вида а1х1+а2х3+…+ аnхn=b (2)Где все коэффициенты и неизвестные –целые числа и хотя бы одно аi≠0.
Определение. Решением диофантова уравнения (2) называется комплекс целых чисел (х1’,x2’,…xn’) удовлетворяющий этому уравнению.
Теорема. При взаимно-простых коэффициентах а1,а2… аn диофантово уравнение а1х1+а2х3+…+ аnхn =1 (3)
Имеет решение в целых числах.
Теорема. Пусть d-НОД коэффициентов а1,а2… аn. Диофантово уравнение (2)имеет решение тогда и только тогда, когда d|b. Число решений такого уравнения равно либо 0, либо бесконечности.
Теорема. Пусть d-НОД a и b, где a≠0,b≠0 и ((х0,у0))- некоторое решение диофантова уравнения: ax+by=с (4)
Тогда множество решений уравнения (4) в целых числах совпадают со множеством комплексов ((x’,y’)) где x’= 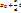 , y’=
, y’= 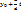 , t-любое целое число.
, t-любое целое число.
30.Системы линейных сравнений. Системы сравнений первой степени с взаимно-простыми модулями .
Определение. Системой линейных сравнений с одним неизвестным (переменным) называется система вида:
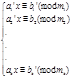 (1)
(1)
Система (1) называется совместной, если она имеет по меньшей мере одно решение. Может получиться, что какое-либо уравнение системы (1) не имеет решений, тогда и система (1) не имеет решения, т.е. несовместна.
Правда возможно, что система может оказаться несовместной и тогда, когда каждое её сравнение разрешимо.
Таким образом, первым шагом на пути разрешимости системы (1) является разрешение каждого сравнения этой системы. Т.е. прежде всего систему приводят к виду (считаем, что все сравнения системы разрешимы):
 (2)
(2)
Теорема. Если система (2) совместна, то она имеет единственное решение по модулю М, равному наименьшему общему кратному чисел 
Доказательство. Первому сравнению системы (2) удовлетворяют числа вида  где
где  Из них одновременно удовлетворяют второму сравнению те числа, для которых
Из них одновременно удовлетворяют второму сравнению те числа, для которых 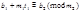 (*)
(*)
Отсюда  . Пусть
. Пусть  Если
Если 
 , то сравнение (*) не имеет решения. Если
, то сравнение (*) не имеет решения. Если  , то перейдём к сравнению
, то перейдём к сравнению  , где
, где 
Это сравнение имеет единственное решение  или
или  Следовательно, первым двум сравнениям
Следовательно, первым двум сравнениям
Системы (2) удовлетворяют значения  , но
, но  Обозначим
Обозначим 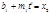 , тогда
, тогда  или
или 
Рассуждая аналогично, переходим к 3-му и т.д. к к-му сравнению. В случае разрешимости системы, ей удовлетворяет класс вычетов по модулю  , который и называют решением системы сравнений (2).Будем сначала считать, что модули в системе (2)
, который и называют решением системы сравнений (2).Будем сначала считать, что модули в системе (2)  взаимно просты. Тогда справедлива
взаимно просты. Тогда справедлива
31. Китайская теорема об остатках (КТО ).
Теорема. Если модули  попарно взаимно-просты, то система сравнений (2) имеет единственное решение по модулю
попарно взаимно-просты, то система сравнений (2) имеет единственное решение по модулю 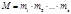 , которое находится по формуле
, которое находится по формуле  , где
, где 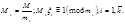
Доказательство. Обозначим 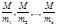 соответственно
соответственно  . Каждое из сравнений:
. Каждое из сравнений:  имеет единственное решение
имеет единственное решение  , так как
, так как 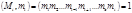 . Будем утверждать, что
. Будем утверждать, что  – решение системы (2).В самом деле,
– решение системы (2).В самом деле,  , так как члены
, так как члены  при
при  кратны
кратны 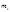 , т.е. сравнимы с нулём по модулю
, т.е. сравнимы с нулём по модулю 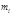 . В правой части (3) можно заменить
. В правой части (3) можно заменить 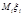 единицей, т.к..
единицей, т.к..  Следовательно,
Следовательно, 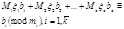 т.е. число
т.е. число  оказалось решением системы (2). Тем самым система (2) имеет единственное решение по модулю
оказалось решением системы (2). Тем самым система (2) имеет единственное решение по модулю  , т.к. наименьшее общее кратное попарно взаимно-простых чисел
, т.к. наименьшее общее кратное попарно взаимно-простых чисел  равно их произведению
равно их произведению  .Таким образом, мы показали, что, если в системе (2) модули взаимно-просты, то такая система всегда имеет решение, причём единственное по модулю
.Таким образом, мы показали, что, если в системе (2) модули взаимно-просты, то такая система всегда имеет решение, причём единственное по модулю  , которое находится по формуле
, которое находится по формуле 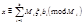 .
.
32. Системы сравнений первой степени, общий случай решения.
Будем теперь рассматривать случаи, когда модули  не являются взаимно-простыми. Выясни, при каких условиях система (2) совместна.
не являются взаимно-простыми. Выясни, при каких условиях система (2) совместна.
Теорема. Если  – каноническое разложение модуля
– каноническое разложение модуля  на простые множители, то сравнение
на простые множители, то сравнение 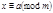 (3) равносильно системе сравнений
(3) равносильно системе сравнений
 (4)
(4)
Доказательство.
Если  какое-нибудь решение данного сравнения, то
какое-нибудь решение данного сравнения, то  делит
делит 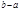 , откуда и подавно
, откуда и подавно  делит
делит 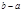 , т.е.
, т.е. 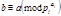 , т.е.
, т.е. 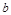 - решение системы (4). Обратно, если
- решение системы (4). Обратно, если  – решение системы сравнений (4), то
– решение системы сравнений (4), то  так как очевидно,
так как очевидно,  есть также решение системы(4) и наименьшее общее кратное чисел
есть также решение системы(4) и наименьшее общее кратное чисел  равно
равно 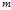 . Отсюда следует,
. Отсюда следует,  - решение сравнения х
- решение сравнения х 
Следствие. Система сравнений (2) равносильна системе сравнений
 (5)
(5)
где 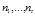 - степени простых множителей канонических разложений модулей
- степени простых множителей канонических разложений модулей 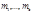
Теорема. Система сравнений (2) совместна тогда и только тогда, когда 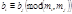 ,
,  (6)
(6)
Доказательство. Пусть система сравнений (2) совместна, т.е. имеет какое-то решение  Тогда
Тогда  Так как
Так как  делит
делит  и
и 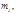 то и тем более
то и тем более 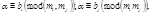 откуда
откуда  Обратно, пусть выполняются условия (6). Тогда согласно вышеизложенному следствию, система сравнений (2) равносильна системе сравнений (5), причём из условий (6) следует, что
Обратно, пусть выполняются условия (6). Тогда согласно вышеизложенному следствию, система сравнений (2) равносильна системе сравнений (5), причём из условий (6) следует, что  так как
так как 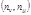 делит
делит 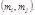
Представляются 2 случая:
1)либо  и
и 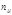 - степени одного и того же простого числа;
- степени одного и того же простого числа;
2)либо 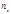 и
и  - степени различных простых чисел.
- степени различных простых чисел.
В первом случае сравнения  системы (5) принимают следующий вид:
системы (5) принимают следующий вид:
 (7)
(7)
 (8), где
(8), где  - некоторое простое число. Пусть, например,
- некоторое простое число. Пусть, например,  Тогда всякое решение сравнения (7) будет также и решением сравнения (8). Действительно, если
Тогда всякое решение сравнения (7) будет также и решением сравнения (8). Действительно, если  - решение сравнения (7), то
- решение сравнения (7), то  а поэтому и подавно
а поэтому и подавно  Но
Но  в силу чего условие
в силу чего условие 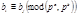 примет вид
примет вид 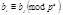 Отсюда
Отсюда  т.е.
т.е. 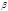 - решение сравнения (8). Во втором случае
- решение сравнения (8). Во втором случае 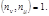
Тогда в системе (5) мы имеем сравнения с попарно взаимно-простыми модулями. Такая система сравнений совместна и имеет единственное решение по модулю, равному произведению модулей этой системы. Следовательно, совместна и первоначальная система (2).
33. Методы решения систем линейных сравнений по простому модулю: возможность переноса методов решения систем линейных уравнений, метод Гаусса, метод Крамера, матричный метод.
Существует возможность перенести известные способы решения систем линейных уравнений на системы линейных сравнений по простому модулю. Пусть имеется система линейных сравнений по простому модулю:






 (*)
(*)
Метод Крамера для решения систем линейных сравнений имеет те же ограничения (с учётом замены отношения равенства отношением сравнимости), что и для систем линейных уравнений. Поэтому для решения системы сравнений этим методом потребуем, чтобы:
а) число сравнений системы было равно числу неизвестных системы, т.е. 
б) определитель 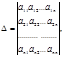 составленный из коэффициентов, при неизвестных был не сравним с нулём по модулю
составленный из коэффициентов, при неизвестных был не сравним с нулём по модулю  Тогда система сравнений имеет единственное решение и оно находится по формулам:
Тогда система сравнений имеет единственное решение и оно находится по формулам:  или
или 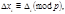 где
где  определитель, полученный из определителя
определитель, полученный из определителя 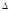 заменой i-ого столбца столбцом свободных членов, т.е.
заменой i-ого столбца столбцом свободных членов, т.е. 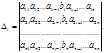
Здесь также необходимо помнить, что определители 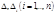 вычисляются по
вычисляются по 
Систему сравнений (*) также можно записать в матричной форме: 
Замечание. Выяснение вопроса о совместности системы линейных сравнений решается так же, как и для систем линейных уравнений по теореме Кронекера-Капелли. Здесь также справедлива и теорема о числе решений, с учётом указанной поправки на случай, если ранг матрицы r системы меньше числа неизвестных n в системе линейных сравнений, то система по данному модулю имеет p решений. Пусть вновь имеется система линейных сравнений по простому модулю (*). Но здесь уже на m и n не накладывается никаких ограничений, т.е.  Рассмотрим решение таких систем сравнений методом Гаусса. Для этого, как и для систем уравнений, составляем расширенную матрицу данной системы:
Рассмотрим решение таких систем сравнений методом Гаусса. Для этого, как и для систем уравнений, составляем расширенную матрицу данной системы:

С помощью элементарных преобразований сводим эту матрицу к ступенчатому виду. Здесь отличие состоит только в том, что
при элементарных преобразованиях коэффициенты  заменяем наименьшими вычетами по
заменяем наименьшими вычетами по  По-прежнему справедливы следующие высказывания, которые являются аналогами высказываний о решении систем линейных уравнений:
По-прежнему справедливы следующие высказывания, которые являются аналогами высказываний о решении систем линейных уравнений:
- если в матрице при элементарных преобразованиях получилась строчка, в которой все  то такая система сравнений несовместна;
то такая система сравнений несовместна;
- если матрица свелась к треугольному виду, то система сравнений имеет единственное решение, которое находим, составляя систему сравнений по треугольной матрице и решая её снизу вверх;
- если матрица свелась к трапециедальному виду, то система сравнений по 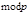 имеет ровно
имеет ровно  решений. Чтобы найти эти решения, по полученной трапециедальной матрице составляем систему сравнений, при этом число сравнений
решений. Чтобы найти эти решения, по полученной трапециедальной матрице составляем систему сравнений, при этом число сравнений  меньше числа неизвестных
меньше числа неизвестных  Тогда из последнего уравнения выражаем
Тогда из последнего уравнения выражаем  считая остальные
считая остальные 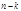 неизвестных свободными, которые могут принимать любые значения из множества классов вычетов по
неизвестных свободными, которые могут принимать любые значения из множества классов вычетов по 
Свободные неизвестные переносим во всех сравнениях системы в правую часть и решаем систему снизу вверх. При этом решение системы сравнений получим в виде:
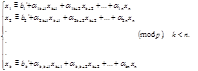
Это и есть общее решение системы сравнений. Всего же получим  решений, за счёт того, что
решений, за счёт того, что 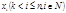 может принимать
может принимать 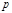 различных значений.
различных значений.
Именно здесь проявляется различие в решении систем линейных уравнений и линейных сравнений. Если матрица сводится к трапециедальному виду, то система уравнений имеет бесконечное множество решений. Объясняется это тем, что решение систем уравнений проводится в поле действительных чисел, которое имеет нулевую характеристику, т.е. содержит бесчисленное множество элементов. Но, не смотря на различия в характеристике полей действительных чисел и классов вычетов по простому модулю, перенесение методов решения систем линейных уравнений на решение систем линейных сравнений оказалось возможным.
34.Сравнения высших степеней по простому модулю, теоремы о равносильности сравнений.
Сравнение по простому модулю представляют собой наиболее простой случай сравнения, но наиболее важный, так как решения сравнений по составному модулю можно свести к решению сравнений по простому модулю.
Пусть дано сравнение 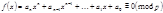 (1)
(1)
где  . При и решении подобных сравнений будем пользоваться следующими теоремами.
. При и решении подобных сравнений будем пользоваться следующими теоремами.
Теорема 1 Сравнение (1) равносильно сравнению 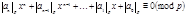 .
.
Например, сравнение  равносильно сравнению
равносильно сравнению  или сравнению
или сравнению 
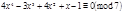
Теорема 2 Если  , то сравнение (1) может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.
, то сравнение (1) может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.
Доказательство. Рассмотрим сравнение  Т.к.
Т.к.  , то
, то  , следовательно сравнение имеет единственное решение. Пусть
, следовательно сравнение имеет единственное решение. Пусть  - решение (2), тогда
- решение (2), тогда  . Умножим сравнение (1) на
. Умножим сравнение (1) на  :
:
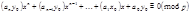 Сравнение (3) равносильно сравнению
Сравнение (3) равносильно сравнению  , где
, где  .
.
Теорема 3 Если  и
и  - многочлены с целыми коэффициентами, то сравнение по простому модулю
- многочлены с целыми коэффициентами, то сравнение по простому модулю 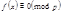 (4) и
(4) и  (5) эквивалентны.
(5) эквивалентны.
Доказательство. Пусть 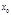 удовлетворяет сравнению (4), т.е.
удовлетворяет сравнению (4), т.е.  . По теореме Ферм
. По теореме Ферм  , следовательно
, следовательно  .Пусть
.Пусть 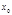 удовлетворяет (5), т.е
удовлетворяет (5), т.е  или
или  . Но по теореме Ферма
. Но по теореме Ферма  , следовательно
, следовательно 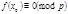 Теорема 4 Сравнению по простому модулю, степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньше чем
Теорема 4 Сравнению по простому модулю, степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньше чем 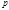 . Доказательство. Пусть
. Доказательство. Пусть 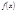 - многочлен с целыми коэффициентами степени
- многочлен с целыми коэффициентами степени  . Тогда по теореме о делении с остатком
. Тогда по теореме о делении с остатком  , где
, где 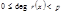 . По теореме 3 сравнение
. По теореме 3 сравнение 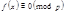 и
и 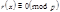 эквивалентны.
эквивалентны.

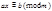 нужно:
нужно: решений, то перейти к сравнению (5) и найти его решение
решений, то перейти к сравнению (5) и найти его решение 
 Преобразованиям можно подвергать
Преобразованиям можно подвергать  или,
или,  а также
а также  и
и  сразу.
сразу. числа, кратного модулю;
числа, кратного модулю; и
и  к сравнимым с ними числам, у которых есть общий делитель.
к сравнимым с ними числам, у которых есть общий делитель. решением сравнения
решением сравнения  является класс
является класс  (7).
(7). 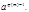

 при
при 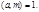 Поэтому получае
Поэтому получае 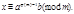
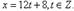

 последовательность подходящихдробей разложения
последовательность подходящихдробей разложения 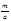 в цепную дробь и
в цепную дробь и 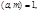 то решением сравнения
то решением сравнения  является класс
является класс 
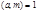 и, учитывая, что подходящие дроби несократимы, то из равенства
и, учитывая, что подходящие дроби несократимы, то из равенства  следует, что
следует, что  По свойству подходящих дробей
По свойству подходящих дробей  Тогда
Тогда  или
или  или
или 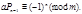 Умножим на
Умножим на  получим
получим  или
или 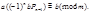 Отсюда следует, что число
Отсюда следует, что число  удовлетворяет данному сравнению, т.е.
удовлетворяет данному сравнению, т.е. 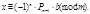
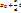 , y’=
, y’= 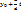 , t-любое целое число.
, t-любое целое число.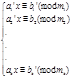 (1)
(1) (2)
(2)
 где
где  Из них одновременно удовлетворяют второму сравнению те числа, для которых
Из них одновременно удовлетворяют второму сравнению те числа, для которых 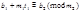 (*)
(*) . Пусть
. Пусть  Если
Если 
 , то сравнение (*) не имеет решения. Если
, то сравнение (*) не имеет решения. Если  , то перейдём к сравнению
, то перейдём к сравнению  , где
, где 
 или
или  Следовательно, первым двум сравнениям
Следовательно, первым двум сравнениям  , но
, но  Обозначим
Обозначим 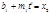 , тогда
, тогда  или
или 
 , который и называют решением системы сравнений (2).Будем сначала считать, что модули в системе (2)
, который и называют решением системы сравнений (2).Будем сначала считать, что модули в системе (2)  взаимно просты. Тогда справедлива
взаимно просты. Тогда справедлива попарно взаимно-просты, то система сравнений (2) имеет единственное решение по модулю
попарно взаимно-просты, то система сравнений (2) имеет единственное решение по модулю 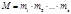 , которое находится по формуле
, которое находится по формуле  , где
, где 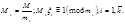
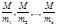 соответственно
соответственно  . Каждое из сравнений:
. Каждое из сравнений:  имеет единственное решение
имеет единственное решение  , так как
, так как 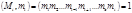 . Будем утверждать, что
. Будем утверждать, что  – решение системы (2).В самом деле,
– решение системы (2).В самом деле,  , так как члены
, так как члены  при
при  кратны
кратны 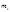 , т.е. сравнимы с нулём по модулю
, т.е. сравнимы с нулём по модулю 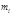 . В правой части (3) можно заменить
. В правой части (3) можно заменить 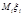 единицей, т.к..
единицей, т.к..  Следовательно,
Следовательно, 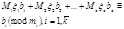 т.е. число
т.е. число  оказалось решением системы (2). Тем самым система (2) имеет единственное решение по модулю
оказалось решением системы (2). Тем самым система (2) имеет единственное решение по модулю  , т.к. наименьшее общее кратное попарно взаимно-простых чисел
, т.к. наименьшее общее кратное попарно взаимно-простых чисел  .Таким образом, мы показали, что, если в системе (2) модули взаимно-просты, то такая система всегда имеет решение, причём единственное по модулю
.Таким образом, мы показали, что, если в системе (2) модули взаимно-просты, то такая система всегда имеет решение, причём единственное по модулю  , которое находится по формуле
, которое находится по формуле 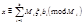 .
. – каноническое разложение модуля
– каноническое разложение модуля  на простые множители, то сравнение
на простые множители, то сравнение 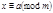 (3) равносильно системе сравнений
(3) равносильно системе сравнений (4)
(4) какое-нибудь решение данного сравнения, то
какое-нибудь решение данного сравнения, то 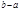 , откуда и подавно
, откуда и подавно  делит
делит 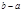 , т.е.
, т.е. 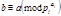 , т.е.
, т.е. 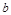 - решение системы (4). Обратно, если
- решение системы (4). Обратно, если  так как очевидно,
так как очевидно,  равно
равно 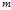 . Отсюда следует,
. Отсюда следует,  - решение сравнения х
- решение сравнения х 
 (5)
(5)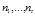 - степени простых множителей канонических разложений модулей
- степени простых множителей канонических разложений модулей 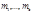
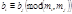 ,
,  (6)
(6) Тогда
Тогда  Так как
Так как  делит
делит  и
и 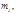 то и тем более
то и тем более 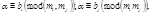 откуда
откуда  Обратно, пусть выполняются условия (6). Тогда согласно вышеизложенному следствию, система сравнений (2) равносильна системе сравнений (5), причём из условий (6) следует, что
Обратно, пусть выполняются условия (6). Тогда согласно вышеизложенному следствию, система сравнений (2) равносильна системе сравнений (5), причём из условий (6) следует, что  так как
так как 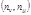 делит
делит 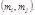
 и
и 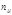 - степени одного и того же простого числа;
- степени одного и того же простого числа;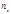 и
и  - степени различных простых чисел.
- степени различных простых чисел. системы (5) принимают следующий вид:
системы (5) принимают следующий вид: (7)
(7) (8), где
(8), где  - некоторое простое число. Пусть, например,
- некоторое простое число. Пусть, например,  Тогда всякое решение сравнения (7) будет также и решением сравнения (8). Действительно, если
Тогда всякое решение сравнения (7) будет также и решением сравнения (8). Действительно, если  - решение сравнения (7), то
- решение сравнения (7), то  а поэтому и подавно
а поэтому и подавно  Но
Но  в силу чего условие
в силу чего условие 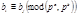 примет вид
примет вид 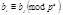 Отсюда
Отсюда  т.е.
т.е. 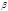 - решение сравнения (8). Во втором случае
- решение сравнения (8). Во втором случае 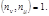


 (*)
(*)
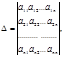 составленный из коэффициентов, при неизвестных был не сравним с нулём по модулю
составленный из коэффициентов, при неизвестных был не сравним с нулём по модулю  Тогда система сравнений имеет единственное решение и оно находится по формулам:
Тогда система сравнений имеет единственное решение и оно находится по формулам:  или
или 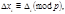 где
где  определитель, полученный из определителя
определитель, полученный из определителя 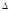 заменой i-ого столбца столбцом свободных членов, т.е.
заменой i-ого столбца столбцом свободных членов, т.е. 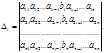
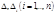 вычисляются по
вычисляются по 

 Рассмотрим решение таких систем сравнений методом Гаусса. Для этого, как и для систем уравнений, составляем расширенную матрицу данной системы:
Рассмотрим решение таких систем сравнений методом Гаусса. Для этого, как и для систем уравнений, составляем расширенную матрицу данной системы:
 заменяем наименьшими вычетами по
заменяем наименьшими вычетами по  По-прежнему справедливы следующие высказывания, которые являются аналогами высказываний о решении систем линейных уравнений:
По-прежнему справедливы следующие высказывания, которые являются аналогами высказываний о решении систем линейных уравнений: то такая система сравнений несовместна;
то такая система сравнений несовместна;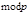 имеет ровно
имеет ровно  решений. Чтобы найти эти решения, по полученной трапециедальной матрице составляем систему сравнений, при этом число сравнений
решений. Чтобы найти эти решения, по полученной трапециедальной матрице составляем систему сравнений, при этом число сравнений  меньше числа неизвестных
меньше числа неизвестных  Тогда из последнего уравнения выражаем
Тогда из последнего уравнения выражаем  считая остальные
считая остальные 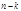 неизвестных свободными, которые могут принимать любые значения из множества классов вычетов по
неизвестных свободными, которые могут принимать любые значения из множества классов вычетов по 
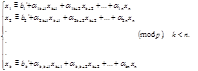
 решений, за счёт того, что
решений, за счёт того, что 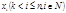 может принимать
может принимать 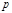 различных значений.
различных значений.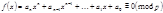 (1)
(1) . При и решении подобных сравнений будем пользоваться следующими теоремами.
. При и решении подобных сравнений будем пользоваться следующими теоремами.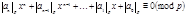 .
. равносильно сравнению
равносильно сравнению  или сравнению
или сравнению 
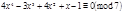
 , то сравнение (1) может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.
, то сравнение (1) может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице. Т.к.
Т.к.  , то
, то  , следовательно сравнение имеет единственное решение. Пусть
, следовательно сравнение имеет единственное решение. Пусть  - решение (2), тогда
- решение (2), тогда  . Умножим сравнение (1) на
. Умножим сравнение (1) на  :
: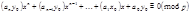 Сравнение (3) равносильно сравнению
Сравнение (3) равносильно сравнению  , где
, где  .
. и
и  - многочлены с целыми коэффициентами, то сравнение по простому модулю
- многочлены с целыми коэффициентами, то сравнение по простому модулю 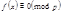 (4) и
(4) и  (5) эквивалентны.
(5) эквивалентны.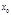 удовлетворяет сравнению (4), т.е.
удовлетворяет сравнению (4), т.е.  . По теореме Ферм
. По теореме Ферм  , следовательно
, следовательно  .Пусть
.Пусть 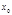 удовлетворяет (5), т.е
удовлетворяет (5), т.е  . Но по теореме Ферма
. Но по теореме Ферма  , следовательно
, следовательно 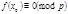 Теорема 4 Сравнению по простому модулю, степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньше чем
Теорема 4 Сравнению по простому модулю, степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньше чем 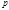 . Доказательство. Пусть
. Доказательство. Пусть 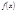 - многочлен с целыми коэффициентами степени
- многочлен с целыми коэффициентами степени  . Тогда по теореме о делении с остатком
. Тогда по теореме о делении с остатком  , где
, где 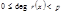 . По теореме 3 сравнение
. По теореме 3 сравнение 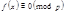 и
и 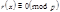 эквивалентны.
эквивалентны.


