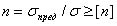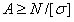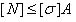Расчеты на прочность при растяжении и сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение
где N — абсолютное значение продольной силы в сечении; А — площадь поперечного сечения; —допускаемое напряжение при растяжении или сжатии для материала стержня. С помощью формулы решается три вида задач (выполняется - три вида расчетов). 1. Проверка прочности (проверочный расчет). При заданных продольной силе N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым непосредственно по формуле. Превышение расчетного (рабочего) напряжения по сравнению с допускаемым не должно быть больше 5 %, иначе прочность рассчитываемой детали считается недостаточной. В случаях, когда рабочие напряжения значительно ниже допускаемых Проверочный расчет деталей машин часто проводят в другой форме. Определяют фактический (расчетный) коэффициент запаса, исходя из известных значений предельного (опасного) напряжения и вычисленного значения рабочего (расчетного) напряжения
2. Подбор сечения (проектный расчет). Исходя из условия, можно определить необходимые размеры сечения, зная продольную силу и допускаемое напряжение. Решив неравенство относительно А, получим
3. Определение допускаемой продольной силы. Допускаемое значение продольной силы в поперечном сечении стержня можно найти по формуле
Допускаемые напряжения назначаются на основе результатов механических испытаний образцов соответствующих материалов.
13. http://www.chirt.ru/download/student/vpo/SP/LR_sopromat_och.pdf
|

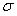 не превосходит допускаемого
не превосходит допускаемого 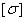 ,
,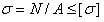
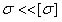 , получаются неэкономичные конструкции с чрезмерным, необоснованным расходом материала. Такие решения являются нерациональными. Следует стремиться к максимальному использованию прочности материала и снижению материалоемкости конструкций.
, получаются неэкономичные конструкции с чрезмерным, необоснованным расходом материала. Такие решения являются нерациональными. Следует стремиться к максимальному использованию прочности материала и снижению материалоемкости конструкций.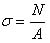 , и сравнивают его с требуемым коэффициентом запаса [n], т. е. условие прочности выражают неравенством
, и сравнивают его с требуемым коэффициентом запаса [n], т. е. условие прочности выражают неравенством