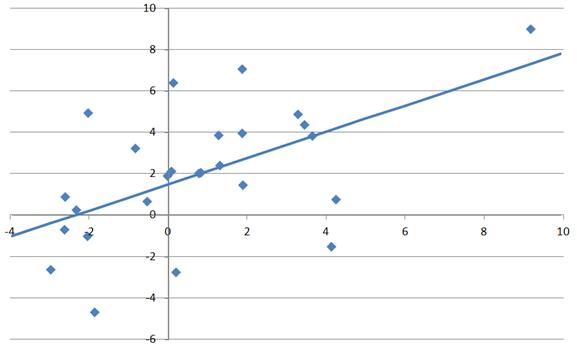
Двумерная выборка. Исходные данные (столбцы xи y): x y x2 y2 x*y 9,18 8,99 84,2724
Задание № 11. Вариант 18
Исходные данные (столбцы xи y):
x
y
x2
y2
x*y
9,18
8,99
84,2724
80,8201
82,5282
-0,01
1,9
0,0001
3,61
-0,019
1,88
7,05
3,5344
49,7025
13,254
3,46
4,37
11,9716
19,0969
15,1202
3,65
3,81
13,3225
14,5161
13,9065
4,14
-1,53
17,1396
2,3409
-6,3342
4,25
0,74
18,0625
0,5476
3,145
3,29
4,86
10,8241
23,6196
15,9894
-2,96
-2,63
8,7616
6,9169
7,7848
0,2
-2,78
0,04
7,7284
-0,556
0,09
2,11
0,0081
4,4521
0,1899
-2,6
0,89
6,76
0,7921
-2,314
1,32
2,4
1,7424
5,76
3,168
1,28
3,84
1,6384
14,7456
4,9152
-0,82
3,23
0,6724
10,4329
-2,6486
-2,32
0,24
5,3824
0,0576
-0,5568
-2,02
4,93
4,0804
24,3049
-9,9586
0,14
6,38
0,0196
40,7044
0,8932
1,89
1,45
3,5721
2,1025
2,7405
0,83
2,06
0,6889
4,2436
1,7098
-2,03
-1,01
4,1209
1,0201
2,0503
1,87
3,94
3,4969
15,5236
7,3678
-2,61
-0,7
6,8121
0,49
1,827
-1,85
-4,71
3,4225
22,1841
8,7135
-0,52
0,65
0,2704
0,4225
-0,338
среднее
0,7892
2,0192
8,424652
14,2454
6,503124
Количество двумерных чисел – 25.
В таблице получены:
- оценки математических ожиданий
mX =0.7892
mY =2.0192
- оценки начальных моментов второго порядка по каждой переменной
- оценка смешанного начального момента второго порядка
На основе этих данных вычислим оценки дисперсий:
Оценка корреляционного момента равна:
XY =5,114137
Точечная оценка коэффициента корреляции равна:
XY =0,551218
Вычислим интервальную оценку коэффициента корреляции с надежностью g=0.95 по формуле:
zg- значение аргумента функции Лапласа, т.е. Ф(zg)=g/2=0.95/2=0.475, которое в нашем случае равно 1.96. Тогда коэффициенты a и b равны:
a=0,202255
b=1,038002
Таким образом, доверительный интервал для коэффициента корреляции имеет вид:
I(RXY )= [0,199541672; 0,777097842]
Проверим гипотезу об отсутствии корреляционной зависимости:
Так как объём выборки невелик (n<50), то определяем значение критерия по следующей формуле:
t=3,168346436
Из таблицы Стьюдента выбираем критическое значение tγ, n-2 , с учётом γ=1-α=0,95.
Значение tγ, n-2 =2,06. Так как t> tγ, n-2 , то гипотеза H0 отклоняется, т.е. величины X и Y коррелированы.
Вычисляем оценки параметров а0и а1линии регрессии
1 =0,629286
0 =1,522568
Уравнение линии регрессии примет вид:
<== предыдущая лекция | следующая лекция ==>
УСТРАНЕНИЕ УТЕЧЕК МАСЛА | Локальная смета на общестроительные работы
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
Этические проблемы проведения экспериментов на человеке и животных В настоящее время четко определены новые подходы и требования к биомедицинским исследованиям...
Классификация потерь населения в очагах поражения в военное время Ядерное, химическое и бактериологическое (биологическое) оружие является оружием массового поражения...
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...

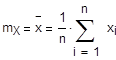
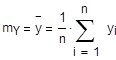


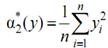



 D(x)=8,126891
D(x)=8,126891 D(y)=10,59191
D(y)=10,59191 KXY=5,114137
KXY=5,114137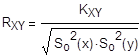 RXY=0,551218
RXY=0,551218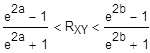
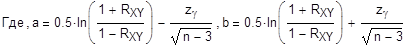


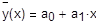 :
: a1=0,629286
a1=0,629286 a0=1,522568
a0=1,522568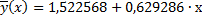 . Построим диаграмму рассеивания и линию регрессии:
. Построим диаграмму рассеивания и линию регрессии: