Студопедия Главная Случайная страница Обратная связь

Разделы: Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Задание 5. Найти выборочное уравнение прямой регрессии Y на X по данной корреляционной таблице.


⇐ Предыдущая12345



Найти выборочное уравнение прямой 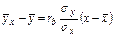регрессии Y на X по данной корреляционной таблице.

1.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

2.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

3.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

4.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

5.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

 

6.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n =100

7.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n = 100

8.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n = 100

9.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n = 100

10.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n = 100

11.

Y X ny
           
      – – – –  
  –     – – –  
  – –       –  
  – –       –  
  – – –        
nx             n = 100

12.

Y X ny
           
      – – – –  
  – –   – –    
  –         –  
  – –       –  
    – – –      
nx             n = 100

13.

Y X ny
             
  – –     – –  
  –   – – –    
    –   –   –  
  –       – –  
    – –   –    
nx             n = 100

14.

Y X ny
           
  – – –     –  
  –     – – –  
  –   –     –  
  – –     –    
    – –     –  
nx             n = 100

15.

Y X ny
           
  – – – –   –  
  –     – – –  
    –       –  
  –         –  
  – – –   –    
nx             n = 100

16.

Y X ny
           
    – – – –    
  –     – – –  
  – –       –  
  –         –  
      – –   –  
nx             n = 100

17.

Y X ny
             
  –   – –   –  
    –   – –    
  –         –  
    –       –  
  – – –        
nx             n = 100

18.

Y X ny
           
  – –   –      
    –   – –    
  – –       –  
  –     –   –  
    – –     –  
nx             n = 100

19.

Y X ny
           
  – –   –      
    –   – – –  
  – –   –      
  –     –   –  
  – – –        
nx             n = 100

20.

Y X ny
           
  – – –   –    
      – – – –  
  – –     – –  
  –     –   –  
  – – –        
nx             n = 100

 




⇐ Предыдущая12345


Дата добавления: 2015-08-12; просмотров: 1323. Нарушение авторских прав; Мы поможем в написании вашей работы!


Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...


Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...


Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...


ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при ко­торых тело находится под действием заданной системы сил...

Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...

Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...

Интуитивное мышление Мышление — это пси­хический процесс, обеспечивающий познание сущности предме­тов и явлений и самого субъекта...

Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...

Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...

Функциональные обязанности медсестры отделения реанимации · Медсестра отделения реанимации обязана осуществлять лечебно-профилактический и гигиенический уход за пациентами...

Studopedia.info - Студопедия - 2014-2026 год . (0.014 сек.) русская версия | украинская версия