Агрегатные индексы
1) Индекс физического объема продукции показывает относительное изменение стоимости продукции из-за изменения объема производства. Агрегатный индекс: где q 1 и q 0 – объем выпуска продаж в базисном и отчетном периодах соответственно; p 0 – цена в базисном периоде. При построении индекса физического объема продукции в качестве соизмерителей (весов) принимаются сопоставимые, неизменные, фиксированные цены, отличающиеся от текущих (действующих) цен (это в условиях инфляции могут быть цены предшествующего периода) или себестоимость продукции z 0. В этом случае индекс характеризует изменение издержек производства.
В зависимости от вида исходных данных можно исчислить средние взвешенные (арифметические и гармонические) индексы физического объема. Если неизвестно q 1, но дано значение q 0 и
Средний гармонический индекс физического объема используется для аналитических оценок в случае, когда неизвестно q 0, но дано значение q 1 и
Пример 9.1. Предприятие выпускает 3 вида неоднородной продукции. Данные об их производстве и ценах на них за два периода приведены в таблице (графы 1–5). Определить индивидуальные и агрегатные индексы физического объема.
Агрегатный индекс физического объема:
Вычитая из числителя знаменатель 2) Индексы цен показывают, как изменилась стоимость продукции за счет изменения цен.
Агрегатный индекс цен Паше (применяется в условиях стабильной экономики):
где p 1 q 1 – фактическая стоимость продаж (товарооборот) в отчетном периоде; p 0 q 1 – условная стоимость товаров, реализованных в отчетном периоде по базисным ценам. Индекс цен Пааше показывает изменение цен отчетного периода по сравнению с базисным (на сколько товары стали дороже (дешевле)). Если бы товары были реализованы в отчетном периоде по базисным ценам, то фактическая экономия составила
Агрегатный индекс цен Ласпейреса (применяется в условиях инфляции):
где p 0 q 0 – фактическая стоимость продаж (товарооборот) в базисном периоде; p 1 q 0 – условная стоимость товаров, реализованных в базисном периоде по отчетным ценам. Индекс цен Ласпейреса показывает условную экономию, т.е. на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде. Этот индекс применяется при прогнозировании объема товарооборота в связи с предлагаемым изменением цен. В условиях стабильности применяют индекс Пааше, при инфляции – индекс Ласпейреса. Основываясь на рассмотренных двух вариантах построения индексов, Фишер предложил рассчитывать среднюю геометрическую индексов цен Пааше и Ласпейреса:
Этот индекс носит название “ идеальный ” индекс цен Фишера. Индекс цен Фишера “обратим” во времени (т.е. если рассчитывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса), но лишен экономического содержания. При синтезировании общего индекса цен вместо фактического количества товаров (в отчетный и базисный периоды) в качестве соизмерителей индексируемых величин р 1 и р 0 могут применяться средние величины реализации товаров. При таком способе расчета формула сводного индекса цен (называемого индексом цен Лоу) выглядит следующим образом:
Индекс цен Лоу применяется в расчетах при закупках или реализации товаров в течение продолжительных периодов времени (пятилетках, десятилетиях и т.п.), поскольку он дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров. Пример 9.2. По имеющимся данным о ценах и реализации неоднородных товаров за два периода необходимо определить индексы цен: 1) индивидуальные; 2) агрегатные, в т.ч. а) индекс Пааше; б) индекс Ласпейреса; в) “идеальный” индекс Фишера; г) индекс Лоу.
Сведем расчет индивидуальных индексов цен и промежуточные расчеты для определения агрегатных индексов цен в таблицу:
а) Индекс цен Пааше
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
т.е. если бы уровень цен остался на уровне базисного периода, экономия потребителя составила бы 250 руб. б) Индекс цен Ласпейреса
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
в) “Идеальный” индекс цен Фишера
г) Индекс цен Лоу
3) Индекс товарооборота (или стоимости продукции), показывает во сколько раз изменилась стоимость продукции. Агрегатный индекс товарооборота
На сколько изменилась стоимость продукции показывает разница между числителем и знаменателем индекса:
Измерить изолированное влияние каждого из этих факторов можно через разность числителя и знаменателя соответствующих аналитических индексов. Разность числителя и знаменателя индекса физического объема (по формуле Ласпейреса)
показывает изменение товарооборота за счет роста (сокращения) физического объема продаж. Разность числителя и знаменателя индекса физического объема (по формуле Пааше)
показывает изменение товарооборота в результате роста (снижения) цен. Абсолютное изменение за счет отдельных факторов в сумме дают общее абсолютное изменение результативного признака:
Участие каждого фактора в формировании общего изменения товарооборота в относительном изменении определяется по следующим формулам: · прирост (уменьшение) товарооборота за счет изменения физического объема продаж
· прирост (уменьшение) товарооборота за счет изменения цен
Совокупное влияние факторов в относительном выражении отражается моделью
При проведении статистического анализа можно определить долю каждого фактора в формировании общего изменения результата: · доля прироста (уменьшения) товарооборота за счет изменения физического объема продаж
· доля прироста (уменьшения) товарооборота за счет изменения цен
При этом Оценка доли отдельных факторов в формировании результата проводится лишь в случае однонаправленного изменения признаков-факторов. 9.4 Средние индексы: индексы переменного и фиксированного состава, индекс структурных сдвигов При изучении качественных показателей часто приходится рассматривать изменение во времени (или пространстве) средней величины индексируемого показателя для определенной совокупности. Будучи сводной характеристикой качественного показателя, средняя величина складывается как под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит объект, так и под влиянием соотношения их весов (“структуры” объекта). Если любой качественный индексируемый показатель обозначить через x, а его веса – через f, то динамику среднего показателя можно отразить как за счет изменения обоих факторов (x и f), так и за счет каждого фактора отдельно. В результате получим три различных индекса: индекс переменного состава, индекс фиксированного состава, индекс структурных сдвигов. Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины x у отдельных элементов (частей целого) и за счет изменения весов f, по которым взвешиваются отдельные значения x. Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям):
Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины x, при фиксировании весов на уровне, как правило отчетного периода f 1: . Другими словами индекс фиксированного состава исключает влияние изменения структуры (состава) совокупности на динамику средних величин, т.е. он характеризует динамику средних величин, рассчитанных для двух периодов при одной и той же фиксированной структуре. Аналогично можно показать динамику среднего показателя лишь за счет изменения весов f при фиксировании индексируемой величины на уровне базисного периода x 0. Такой индекс условно назван индексом структурных сдвигов:
Индекс переменного состава есть произведение индекса фиксированного состава на индекс структурных сдвигов:
Пример 9.3. По имеющимся данным о выпуске и ценах одноименного товара на двух предприятиях требуется определить изменение стоимости единицы продукции на каждом предприятии, а также в целом по всем предприятиям с помощью индексов: а) переменного состава; б) фиксированного состава; в) структурных сдвигов.
Индивидуальные индексы для 1-го и 2-го предприятия соответственно:
Для дальнейших расчетов понадобятся дополнительные расчеты:
Средние себестоимости: в базисном периоде в отчетном периоде Индекс переменного состава:
Индекс фиксированного состава:
Индекс структурных сдвигов:
Проверка 1.26*1.056=1.33 Себестоимость по двум предприятиям в среднем выросла на 33% I пc – 100% = 133 – 100 =33%. В том числе: · за счет изменения структуры выпуска продукции: I cc – 100% = 105,6 – 100 = 5,6%; · за счет снижения себестоимости на каждом предприятии I пc – I cc = 1,26 – 100= –1,82%.
|

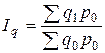 , (9.2)
, (9.2)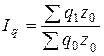 . (9.3)
. (9.3)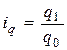 , а также стоимость продукции базисного периода p 0, то средний арифметический индекс физического объема равен:
, а также стоимость продукции базисного периода p 0, то средний арифметический индекс физического объема равен: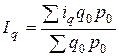 . (9.4)
. (9.4)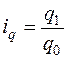 , а также стоимость продукции базисного периода p 0:
, а также стоимость продукции базисного периода p 0: . (9.5)
. (9.5)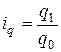
 = 0,773(77,3%).
= 0,773(77,3%).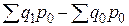 = 1275-1650= –375 тыс. руб., определяем, что в абсолютном выражении за счет уменьшения выпуска стоимость продукции в отчетном периоде уменьшилась на 375 тыс.руб.
= 1275-1650= –375 тыс. руб., определяем, что в абсолютном выражении за счет уменьшения выпуска стоимость продукции в отчетном периоде уменьшилась на 375 тыс.руб.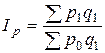 , (9.6)
, (9.6)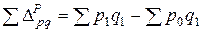 . (9.7)
. (9.7) , (9.8)
, (9.8)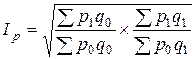 . (9.10)
. (9.10)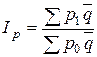 . (9.11)
. (9.11)
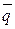
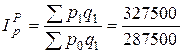 = 1,018 (101,8%).
= 1,018 (101,8%).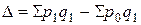 = 14000-13750=250 руб.,
= 14000-13750=250 руб.,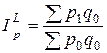
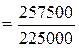 = 1,06(106%).
= 1,06(106%).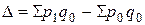 = 13250-12500= 750 руб.
= 13250-12500= 750 руб.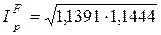 =1,039 (103,9%).
=1,039 (103,9%).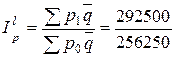 = 1,039(103,9%).
= 1,039(103,9%).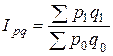 . (9.12)
. (9.12)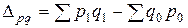 . (9.13)
. (9.13)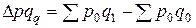 (9.14)
(9.14) (9.15)
(9.15)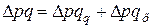 . (9.16)
. (9.16)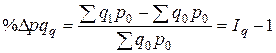 ; (9.17)
; (9.17)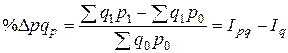 . (9.18)
. (9.18)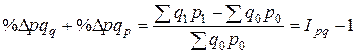 . (9.19)
. (9.19) ; (9.20)
; (9.20) . (9.21)
. (9.21) (или 100%). (9.22)
(или 100%). (9.22)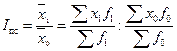 . (9.23)
. (9.23)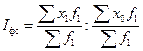 (9.24)
(9.24)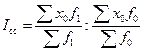 . (9.25)
. (9.25)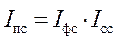 . (9.26)
. (9.26)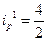 = 2 (200%);
= 2 (200%); 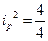 = 1 (100%).
= 1 (100%).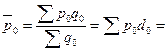 3ру б.;
3ру б.;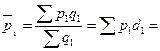 4 руб.
4 руб. 1.33
1.33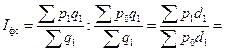 1.26
1.26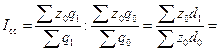 1.056
1.056


