Матрица линейного оператора
В силу теоремы 5.4 линейный оператор в конечномерном линейном пространстве однозначно можно задать при помощи образов базисных векторов. Наряду с ядром, образом, дефектом и рангом для линейного оператора имеет место такая характеристика, как матрица этого оператора. Пусть
Разложим векторы
где Определение 5.6. Квадратная матрица
столбцами которой являются координатные вектор-столбцы векторов Следующая теорема позволяет найти координаты образа в базисе через матрицу оператора и координаты прообраза в том же базисе. Теорема 5.7. Пусть
матрицы □ Пусть в базисе
Учитывая, что образы
получим
В силу того, что разложение вектора
что равносильно матричному равенству (5.1). ■ Матрица линейного оператора изменяется, когда изменяется базис линейного пространства. Найдем связь между матрицами линейного оператора в разных базисах этого линейного пространства. Теорема 5.8 ( о связи матриц линейного оператора в разных базисах ). Пусть
где □ Пусть вектору
где Далее, если
откуда и следует справедливость равенства (5.2). ■ Теорема 5.9. Определитель матрицы линейного оператора не зависит от выбора базиса. □ Пусть оператор
Согласно теореме 5.9 при смене базиса линейного пространства изменяется матрица оператора, а определитель её при этом остается неизменным. Значит, этот определитель характеризует не конкретную матрицу оператора в данном базисе, а сам оператор. Это позволяет ввести следующее определение. Определение 5.7. Определителем линейного оператора, действующего в линейном пространстве, называется определитель матрицы этого оператора в любом базисе. Теорема 5.10. Ранг линейного оператора совпадает с рангом матрицы этого оператора. Пример 5.1. Записать матрицу линейного оператора
в базисе Найти образ, ранг, ядро, дефект, базисы образа и ядра оператора. Решение. Находим образы
Для составления матрицы
Каждое из уравнений этой системы решаем отдельно. Первое уравнение можно переписать в виде
Решая его, получим вектор-столбец координат вектора
Решая аналогично остальные два уравнения, получим координатные вектор-столбцы векторов
В результате матрица
Для нахождения ядра
Очевидно, что размерность ядра (дефект оператора) равна
базисный вектор в ядре
Размерность образа оператора (ранг оператора) равна
Для нахождения базиса образа
Из вида ступенчатой матрицы следует, что базис образа
|

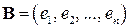 – базис в конечномерном линейном пространстве
– базис в конечномерном линейном пространстве 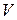 (
(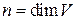 ). Тогда по теореме 5.4 для любых векторов
). Тогда по теореме 5.4 для любых векторов  существует единственный линейный оператор
существует единственный линейный оператор 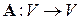 , переводящий векторы
, переводящий векторы  базиса
базиса 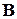 в соответствующие векторы
в соответствующие векторы 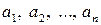 , что можно записать в виде следующей операторной системы:
, что можно записать в виде следующей операторной системы:
 через векторы базиса
через векторы базиса 
 – некоторые числа.
– некоторые числа. ,
,

 в базисе
в базисе 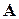 в базисе
в базисе  линейный оператор, действующий в линейном пространстве
линейный оператор, действующий в линейном пространстве  базис в
базис в  координат вектора
координат вектора 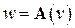 равен произведению
равен произведению (5.1)
(5.1) оператора в данном базисе на вектор-столбец
оператора в данном базисе на вектор-столбец  координат вектора
координат вектора  в данном базисе.
в данном базисе. через базисные векторы
через базисные векторы
 базисных векторов базиса
базисных векторов базиса  ,
,
 по базису
по базису 
 – базисы в линейном пространстве
– базисы в линейном пространстве 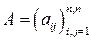 и
и  оператора
оператора  связаны равенством
связаны равенством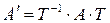 , (5.2)
, (5.2) – матрица перехода от базиса
– матрица перехода от базиса  , а вектору
, а вектору  вектор-столбцы
вектор-столбцы  . Тогда в силу матричного равенства (5.1), имеем
. Тогда в силу матричного равенства (5.1), имеем ,
,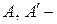 матрицы линейного оператора
матрицы линейного оператора 
 . Тогда на основании равенства (5.2) и свойств определителей имеем
. Тогда на основании равенства (5.2) и свойств определителей имеем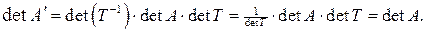 ■
■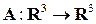 , заданного по правилу
, заданного по правилу

 , где
, где  .
.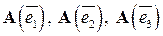 векторов
векторов 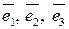 :
: .
.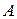 линейного оператора
линейного оператора 

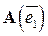 в базисе
в базисе  .
. в базисе
в базисе  ,
,  .
.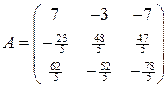 .
. линейного оператора необходимо решить однородную систему уравнений
линейного оператора необходимо решить однородную систему уравнений  с матрицей
с матрицей 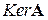 оператора, каждый вектор которого имеет вид
оператора, каждый вектор которого имеет вид .
. ,
, .
. .
. исследуем на линейную зависимость систему векторов
исследуем на линейную зависимость систему векторов  и приведём ее к ступенчатому виду (в результате элементарных преобразований нумерация столбцов не изменялась):
и приведём ее к ступенчатому виду (в результате элементарных преобразований нумерация столбцов не изменялась):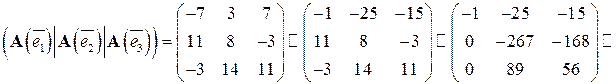

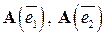 .
.


