| №
| Запитання
| Розділ. Параграф.
|
| 1.
| Обчислити ймовірність попадання похибки в інтервал (0- 3 см), якщо ймовірності попадання в інтервали (0 – 2 см) і (2 – 3 см) відповідно дорівнюють 0,8 і 0,15.
| Р.2:П.2
|
|
| а) 0,8
б) 0,95
в) 0,15
г) 1,0
д) 0
|
|
| 2.
| Обчислити ймовірність попадання похибки в інтервал (0 – 2 см), якщо ймовірність попадання похибки в інтервал (0 – 1 см) дорівнює 0,65, а ймовірність попадання в інтервал (1 – 2 см) дорівнює 0,20.
| Р.2:П.2
|
|
| а) 0,20
б) 0,65
в) 1,0
г) 0,85
д) 0
|
|
| 3.
| Ймовірність попадання похибки в інтервал (0 – 1 см) дорівнює 0,6, в інтервал (1 – 2 см) дорівнює 0,20, в інтервал (2 – 3 см) дорівнює 0,15, в інтервал (3 – 4 см) дорівнює 0,03. Обчислити ймовірність попадання похибки або в інтервал (0 – 1 см), або в інтервал (3 – 4 см).
| Р.2:П.2
|
|
| а) 0,63
б) 0,20
в) 0,15
г) 1,00
д) 0
|
|
| 4.
| Обчислити ймовірність того, що при двох вимірах з'явиться або додатня і від'ємна, або від'ємна і додатня похибки.
| Р.2:П.2
|
|
| а) 0,25
б) 0,9
в) 0,5
г) 1,0
д) 0
|
|
| 5.
| В урні знаходяться 2 білих, 5 чорних і 3 червоних кулі. Дехто виймає одну кулю. Обчислити ймовірність того, що ця куля буде білою або червоною.
| Р.2:П.2
|
|
| а) 0,2
б) 1,0
в) 0,5
г) 0,3
д) 0
|
|
| 6.
| Проводиться два виміри. Обчислити ймовірність того, що при першому вимірі з’явиться додатня похибка, а при другому - від'ємна.
| Р.2:П.2
|
|
| а) 0,5
б) 1,0
в) 0,75
г) 0,25
д) 0
|
|
| 7.
| Обчислити ймовірність того, що при двох вимірах з’являться дві додатні похибки.
| Р.2:П.2
|
|
| а) 1,0
б) 0,25
в) 0,5
г) 0,75
д) 0
|
|
| 8.
| Проводиться два постріли по мішені. Обчислити ймовірність того, що при першому пострілі буде попадання, а при другому промах.
| Р.2:П.2
|
|
| а) 0,25
б) 0,5
в) 1,0
г) 0,75
д) 0
|
|
| 9.
| Обчислити ймовірність появи білої кулі з урни, в якій знаходяться 4 білі, 2 чорні і 4 сині кулі, при одному витягуванні кулі з урни.
| Р.2:П.1
|
|
| а) 1,0
б) 0,5
в) 0,8
г) 0,4
д) 0
|
|
| 10.
| Обчислити ймовірність появи білої кулі з урни, в якій знаходяться 6 білих, 3 чорні і 3 сині кулі, при одному витягування кулі з урни.
| Р.2:П.1
|
|
| а) 0,25
б) 1,0
в) 0,75
г) 0,5
д) 0
|
|
| 11.
| В урні знаходяться 3 білих, 3 чорних і 6 червоних куль. Дехто виймає одну кулю. Обчислити ймовірність того, що ця куля буде білою або чорною.
| Р.2:П.2
|
|
| а) 0,3
б) 0,5
в) 0,6
г) 1,0
д) 0
|
|
| 12.
| Обчислити ймовірність появи або білої або зеленої кулі з урни, в якій знаходяться 5 білих, 6 чорних і 3 зелені кулі при одному витягуванні кулі з урни.
| Р.2:П.2
|
|
| а) 5/14
б) 3/7
в) 4/7
г) 3/14
д) 0
|
|
| 13.
| Обчислити ймовірність появи числа очок кратного 3 при одному киданні грального кубика.
| Р.2:П.1
|
|
| а) 1/2
б) 1
в) 1/5
г) 1/3
д) 0
|
|
| 14.
| Обчислити ймовірність появи чорної кулі з урни, в якій знаходяться 6 білих, 4 чорних і 4 синіх кулі при одному витягуванні кулі з урни.
| Р.2:П.1
|
|
| а) 1
б) 3/7
в) 2/7
г) 4/7
д) 0
|
|
| 15.
| Обчислити ймовірність появи числа очок кратного 2 при одному киданні грального кубика.
| Р.2:П.1
|
|
| а) 0,25
б) 0,5
в) 0,75
г) 1,0
д) 0
|
|
| 16.
| Обчислити ймовірність появи 2- х або 6- ти очок при одному киданні грального кубика.
| Р.2:П.2
|
|
| а) 1/3
б) 1/2
в) 1
г) 3/4
д) 0
|
|
| 17.
| Обчислити ймовірність появи короля, або дами при одному витягуванні карти з колоди в 24 карти.
| Р.2:П.2
|
|
| а) 1/6
б) 1/3
в) 1
г) 3/4
д) 0
|
|
| 18.
| Обчислити ймовірність появи два рази цифри при двох підкиданнях монети.
| Р.2:П.2
|
|
| а) 0,5
б) 0,25
в) 0,75
г) 1,0
д) 0
|
|
| 19.
| Обчислити ймовірність появи при першому киданні цифри, а при другому герба при двох підкиданнях монети.
| Р.2:П.2
|
|
| а) 1,0
б) 0,75
в) 0,5
г) 0,25
д) 0
|
|
| 20.
| В урні знаходяться 4 білі, 6 чорних куль. Дехто виймає одну кулю. Обчислити ймовірність того, що ця куля буде білою.
| Р.2:П.1
|
|
| а) 1/5
б) 3/5
в) 2/5
г) 1
д) 0
|
|
| 21.
| Обчислити ймовірність появи білої або зеленої кулі з урни, в якій знаходяться 6 білих, 6 чорних і 6 зелених куль при одному витягуванні кулі з урни.
| Р.2:П.2
|
|
| а) 1/3
б) 2/3
в) 1/2
г) 1
д) 0
|
|
| 22.
| Обчислити ймовірність того, що при двох вимірах з'явиться або додатня і від'ємна, або від'ємна і додатня похибки.
| Р.2:П.2
|
|
| а) 0,25
б) 1,0
в) 0,75
г) 0,5
д) 0
|
|
| 23.
| Задано вибірку 4, 2, 5, 1, 5, 2, 4. Знайти вибірковий розмах.
| Р.3:П.1
|
|
| а) 1
б) 4
в) 2
г) 7
д) 0
|
|
| 24.
| Задано вибірку 1, -1, 2, 2, 2, -2, 0. Знайти вибіркову моду.
| Р.3:П.1
|
|
| а) -1
б) -2
в) 2
г) 0
д) 3
|
|
| 25.
| Задано вибірку -1, 2, 0, -2, -1, 1, 1. Знайти вибірковий розмах.
| Р.3:П.1
|
|
| а) 4
б) -1
в) 1
г) 0
д) 2
|
|
| 26.
| Задано вибірку 1; 2; -1; -1; -1; 0; -2. Знайти вибіркову моду.
| Р.3:П.1
|
|
| а) 0
б) -1
в) -2
г) 2
д) 1
|
|
| 27.
| Задано вибірку -4, -1, 1, 1, 4, -1, -1. Знайти вибірковий розмах.
| Р.3:П.1
|
|
| а) 8
б) -4
в) 4
г) 1
д) 0
|
|
| 28.
| Задано вибірку 1; -1; -4; 2; -4; 4. Знайти вибіркову моду.
| Р.3:П.1
|
|
| а) 1
б) -1
в) 2
г) -4
д) 0
|
|
| 29.
| Задано вибірку 3, 2, 2, 0, -3, -2, -2, 3, 3. Знайти вибіркову моду.
| Р.3:П.1
|
|
| а) 0
б) 2
в) 3
г) -2
д) 1
|
|
| 30.
| Задано вибірку 4; -3; 3; 6; -4. Знайти вибірковий розмах.
| Р.3:П.1
|
|
| а) 4
б) 10
в) -3
г) 6
д) 0
|
|
| 31.
| Задано вибірку 2, 1, -1, -1, 1, 2, 2. Знайти вибірковий розмах.
| Р.3:П.1
|
|
| а) 2
б) 3
в) 1
г) -1
д) 0
|
|
| 32.
| Середня квадратична похибка середнього вагового запишеться:
| Р.1:П.11
|
|
| а) 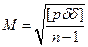 б)
б)  в)
в)  г)
г) 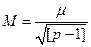 д)
д) 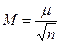
|
|
| 33.
| Середня квадратична похибка середнього арифметичного рівна:
| Р.1:П.7
|
|
| а) 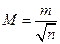 б)
б) 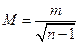 в)
в) 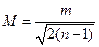 г)
г) 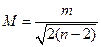 д)
д) 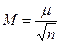
|
|
| 34.
| Середня квадратична похибка різниці двох вимірів знаходиться:
| Р.1:П.6
|
|
| а) 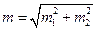 б)
б)  в)
в) 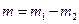 г)
г) 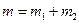 д)
д) 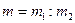
|
|
| 35.
| Вага різниці двох вимірів рівна:
| Р.1:П.10
|
|
| а)  б)
б)  в)
в) 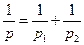 г)
г) 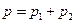 д)
д) 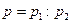
|
|
| 36.
| Дисперсія випадкової величини X рівна:
| Р.2:П.3
|
|
| а) 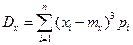 б)
б) 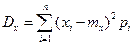 в)
в)  г)
г) 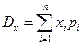 д)
д) 
|
|
| 37.
| Ексцес випадкової величини X знаходиться:
| Р.2:П.3
|
|
| а) 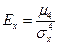 б)
б) 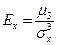 в)
в) 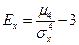 г)
г) 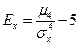 д)
д) 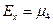
|
|
| 38.
| Математичне сподівання випадкової величини X рівне:
| Р.2:П.3
|
|
| а) 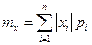 б)
б) 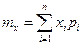 в)
в) 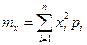 г)
г) 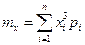 д)
д) 
|
|
| 39.
| Середнє квадратичне відхилення випадкової величини X обчислюється:
| Р.2:П.3
|
|
| а)  б)
б) 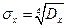 в)
в) 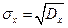 г)
г) 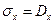 д)
д) 
|
|
| 40.
| Середня квадратична похибка суми двох вимірів знаходиться:
| Р.1:П.6
|
|
| а) 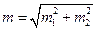 б)
б)  в)
в) 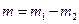 г)
г) 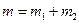 д)
д) 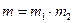
|
|
| 41.
| Вага суми двох вимірів рівна:
| Р.1:П.10
|
|
| а)  б)
б)  в)
в) 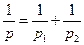 г)
г) 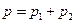 д)
д) 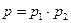
|
|
| 42.
| Кількість параметрів рівна: 7. Кількість поправок до результатів вимірів рівна: 10. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 7
б) 10
в) 3
г) 17
д) 0
|
|
| 43.
| Кількість параметрів рівна: 5. Кількість поправок до результатів вимірів рівна: 7. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 7
б) 5
в) 2
г) 12
д) 0
|
|
| 44.
| Кількість параметрів рівна: 3. Кількість поправок до результатів вимірів рівна: 7. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 3
б) 4
в) 7
г) 10
д) 0
|
|
| 45.
| Кількість параметрів рівна: 2. Кількість поправок до результатів вимірів рівна: 6. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 4
б) 6
в) 2
г) 8
д) 0
|
|
| 46.
| Кількість параметрів рівна: 4. Кількість поправок до результатів вимірів рівна: 6. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 4
б) 2
в) 6
г) 10
д) 0
|
|
| 47.
| Кількість параметрів рівна: 8. Кількість поправок до результатів вимірів рівна: 10. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 10
б) 2
в) 8
г) 18
д) 0
|
|
| 48.
| Кількість параметрів рівна: 5. Кількість поправок до результатів вимірів рівна: 9. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 5
б) 9
в) 4
г) 14
д) 0
|
|
| 49.
| Кількість параметрів рівна: 4. Кількість поправок до результатів вимірів рівна: 10. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 6
б) 4
в) 10
г) 14
д) 0
|
|
| 50.
| Кількість параметрів рівна: 6. Кількість поправок до результатів вимірів рівна: 9. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 9
б) 3
в) 6
г) 15
д) 0
|
|
| 51.
| Кількість параметрів рівна: 15. Кількість поправок до результатів вимірів рівна: 20. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 5
б) 15
в) 20
г) 35
д) 0
|
|
| 52.
| Середня квадратична похибка третього невідомого рівна:
| Р.4:П.5
|
|
| а) 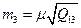 б)
б) 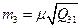 в)
в) 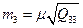 г)
г) 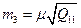 д)
д) 
|
|
| 53.
| Формула мінімуму параметричного методу зрівноважування запишеться:
| Р.4:П.2
|
|
| а)  б)
б) 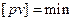 в)
в)  г)
г) 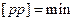 д)
д) 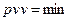
|
|
| 54.
| Принцип найменших квадратів запишеться:
| Р.4:П.1
|
|
| а) 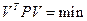 б)
б) 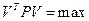 в)
в) 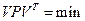 г)
г) 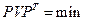 д)
д) 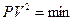
|
|
| 55.
| Середня квадратична похибка першого невідомого рівна:
| Р.4:П.5
|
|
| а) 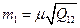 б)
б)  в)
в) 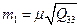 г)
г)  д)
д) 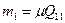
|
|
| 56.
| Середня квадратична похибка другого невідомого рівна:
| Р.4:П.5
|
|
| а) 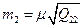 б)
б)  в)
в) 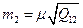 г)
г)  д)
д) 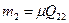
|
|
| 57.
| Кількість параметрів рівна: 10. Кількість поправок до результатів вимірів рівна: 21. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 21
б) 10
в) 11
г) 31
д) 0
|
|
| 58.
| Кількість параметрів рівна: 5. Кількість поправок до результатів вимірів рівна: 15. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 15
б) 10
в) 5
г) 20
д) 0
|
|
| 59.
| Кількість параметрів рівна: 9. Кількість поправок до результатів вимірів рівна: 15. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 9
б) 6
в) 15
г) 24
д) 0
|
|
| 60.
| Кількість параметрів рівна: 7. Кількість поправок до результатів вимірів рівна: 13. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 7
б) 13
в) 6
г) 20
д) 0
|
|
| 61.
| Кількість параметрів рівна: 4. Кількість поправок до результатів вимірів рівна: 11. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 11
б) 4
в) 7
г) 15
д) 0
|
|
| 62.
| Кількість параметрів рівна: 12. Кількість поправок до результатів вимірів рівна: 16. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 4
б) 12
в) 16
г) 28
д) 0
|
|
| 63.
| Кількість параметрів рівна: 5. Кількість поправок до результатів вимірів рівна: 8. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 8
б) 5
в) 3
г) 13
д) 0
|
|
| 64.
| Кількість параметрів рівна: 6. Кількість поправок до результатів вимірів рівна: 10. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 10
б) 4
в) 6
г) 16
д) 0
|
|
| 65.
| Кількість параметрів рівна: 3. Кількість поправок до результатів вимірів рівна: 9. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 9
б) 6
в) 3
г) 12
д) 0
|
|
| 66.
| Кількість параметрів рівна: 9. Кількість поправок до результатів вимірів рівна: 13. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 9
б) 13
в) 4
г) 22
д) 0
|
|
| 67.
| Кількість параметрів рівна: 15. Кількість поправок до результатів вимірів рівна: 19. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 19
б) 4
в) 15
г) 34
д) 0
|
|
| 68.
| Кількість параметрів рівна: 10. Кількість поправок до результатів вимірів рівна: 16. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 10
б) 6
в) 16
г) 26
д) 0
|
|
| 69.
| Кількість параметрів рівна: 8. Кількість поправок до результатів вимірів рівна: 20. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 12
б) 20
в) 8
г) 28
д) 0
|
|
| 70.
| Кількість параметрів рівна: 7. Кількість поправок до результатів вимірів рівна: 12. Кількість параметричних рівнянь рівна:
| Р.4:П.10
|
|
| а) 12
б) 7
в) 5
г) 19
д) 0
|
|
| 71.
| Кількість поправок до результатів вимірів рівна: 10. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 10
в) 3
г) 13
д) 0
|
|
| 72.
| Кількість поправок до результатів вимірів рівна: 9. Кількість нев’язок рівна: 5. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 9
б) 5
в) 4
г) 14
д) 0
|
|
| 73.
| Кількість поправок до результатів вимірів рівна: 7. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 4
в) 3
г) 10
д) 0
|
|
| 74.
| Кількість поправок до результатів вимірів рівна: 11. Кількість нев’язок рівна: 8. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 11
б) 8
в) 3
г) 19
д) 0
|
|
| 75.
| Кількість поправок до результатів вимірів рівна: 15. Кількість нев’язок рівна: 9. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 6
б) 15
в) 9
г) 24
д) 0
|
|
| 76.
| Кількість поправок до результатів вимірів рівна: 16. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 3
б) 16
в) 13
г) 19
д) 0
|
|
| 77.
| Кількість поправок до результатів вимірів рівна: 7. Кількість нев’язок рівна: 5. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 5
в) 2
г) 12
д) 0
|
|
| 78.
| Кількість поправок до результатів вимірів рівна: 14. Кількість нев’язок рівна: 9. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 9
б) 14
в) 5
г) 23
д) 0
|
|
| 79.
| Кількість поправок до результатів вимірів рівна: 17. Кількість нев’язок рівна: 13. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 17
б) 13
в) 4
г) 30
д) 0
|
|
| 80.
| Кількість поправок до результатів вимірів рівна: 10. Кількість нев’язок рівна: 8. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 8
б) 10
в) 2
г) 18
д) 0
|
|
| 81.
| Кількість поправок до результатів вимірів рівна: 7. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 4
в) 3
г) 10
д) 0
|
|
| 82.
| Кількість поправок до результатів вимірів рівна: 11. Кількість нев’язок рівна: 6. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 11
б) 6
в) 5
г) 17
д) 0
|
|
| 83.
| Кількість поправок до результатів вимірів рівна: 5. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 5
б) 2
в) 3
г) 8
д) 0
|
|
| 84.
| Кількість поправок до результатів вимірів рівна: 7. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 4
в) 3
г) 10
д) 0
|
|
| 85.
| Кількість поправок до результатів вимірів рівна: 9. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 9
б) 3
в) 6
г) 12
д) 0
|
|
| 86.
| Кількість поправок до результатів вимірів рівна: 10. Кількість нев’язок рівна: 9. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 9
б) 10
в) 1
г) 19
д) 0
|
|
| 87.
| Кількість поправок до результатів вимірів рівна: 12. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 3
б) 12
в) 9
г) 15
д) 0
|
|
| 88.
| Кількість поправок до результатів вимірів рівна: 6. Кількість нев’язок рівна: 2. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 2
б) 6
в) 4
г) 8
д) 0
|
|
| 89.
| Кількість поправок до результатів вимірів рівна: 10. Кількість нев’язок рівна: 3. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 7
б) 10
в) 3
г) 13
д) 0
|
|
| 90.
| Кількість поправок до результатів вимірів рівна: 20. Кількість нев’язок рівна: 13. Кількість умовних рівнянь рівна:
| Р.4:П.9
|
|
| а) 20
б) 13
в) 7
г) 33
д) 0
|
|