| №
| Запитання
| Розділ. Параграф.
|
| 1.
| Середнє значення кута з 9 прийомів має середню квадратичну похибку Мα=4,0";. Визначити середню квадратичну похибку середнього значення кута Мβ з 16 прийомів при тих же умовах.
| Р.1:П.6
|
|
| а) 1"
б) 3"
в) 5"
г) 7"
д) 0"
|
|
| 2.
| Обчислити середню квадратичну похибку функції U=4z+3x+3, якщо mx=mz=1.
| Р.1:П.6
|
|
| а) 0
б) 5
в) 15
г) 10
д) 1
|
|
| 3.
| Середнє значення кута з 4 прийомів має середню квадратичну похибку Мα=5,0";. Визначити середню квадратичну похибку середнього значення кута Мβ з 25 прийомів при тих же умовах.
| Р.1:П.6
|
|
| а) 10"
б) 7"
в) 5"
г) 2"
д) 0"
|
|
| 4.
| Обчислити середню квадратичну похибку функції U=2x+2y+4z+5, якщо задані похибки аргументів mx=my=mz=1.
| Р.1:П.6
|
|
| а) 5
б) 3
в) 1
г) 9
д) 0
|
|
| 5.
| Середнє значення кута з 64 прийомів має середню квадратичну похибку Мα=2,5";. Визначити середню квадратичну похибку середнього значення кута Мβ з 16 прийомів при тих же умовах.
| Р.1:П.6
|
|
| а) 9"
б) 7"
в) 5"
г) 3"
д) 0"
|
|
| 6.
| Обчислити середню квадратичну похибку функції U=3x+4z+2, якщо задані похибки аргументів mx=mz=1.
| Р.1:П.6
|
|
| а) 0
б) 1
в) 2
г) 5
д) 10
|
|
| 7.
| Середнє значення кута з 81 прийому має середню квадратичну похибку Мα=3,0";. Визначити середню квадратичну похибку середнього значення кута Мβ з 9 прийомів при тих же умовах.
| Р.1:П.6
|
|
| а) 3"
б) 9"
в) 5"
г) 1"
д) 0"
|
|
| 8.
| Обчислити середню квадратичну похибку функції z=8x+6y+4, якщо задані похибки аргументів mx=my=1.
| Р.1:П.6
|
|
| а) 1
б) 5
в) 10
г) 15
д) 0
|
|
| 9.
| Середнє значення кута з 16 прийомів має середню квадратичну похибку Мα=4,5";. Визначити середню квадратичну похибку середнього значення кута Мβ з 4 прийомів при тих же умовах.
| Р.1:П.6
|
|
| а) 9"
б) 6"
в) 3"
г) 1"
д) 0"
|
|
| 10.
| Обчислити середню квадратичну похибку функції U=3x – 4y+z, якщо задані похибки аргументів mx=my=mz=1.
| Р.1:П.6
|
|
| а) 1
б) 2
в) 3
г) 5
д) 0
|
|
| 11.
| Обчислити вагу функції U=5x+2z+5, якщо Рх=25; Рz=4.
| Р.1:П.10
|
|
| а) 1/5
б) 5
в) 2
г) 1/2
д) 0
|
|
| 12.
| Вимір з середньою квадратичною похибкою m1=2,0"; має вагу P1=1. Яка вага відповідає виміру з середньою квадратичною похибкою m2=1,4"?
| Р.1:П.8
|
|
| а) 1
б) 2
в) 5
г) 10
д) 0
|
|
| 13.
| Знайти вагу функції U=2x+2y+z+6, якщо Pz=Py=4; Px=1.
| Р.1:П.10
|
|
| а) 1/3
б) 3
в) 2
г) 1/2
д) 0
|
|
| 14.
| Вимір з середньою квадратичною похибкою m1=4,0"; має вагу P1=3. Яка вага відповідає виміру з середньою квадратичною похибкою m2=2,0"?
| Р.1:П.8
|
|
| а) 2
б) 10
в) 12
г) 15
д) 0
|
|
| 15.
| Знайти вагу функції U=l1+l2 + l3, якщо ваги аргументів дорівнюють P1=P2=P3=1.
| Р.1:П.10
|
|
| а) 1/2
б) 1/5
в) 1/4
г) 1/3
д) 0
|
|
| 16.
| Вимір з середньою квадратичною похибкою m1=1,4"; має вагу P1=8. Яка вага відповідає виміру з середньою квадратичною похибкою m2=4,0"?
| Р.1:П.8
|
|
| а) 10
б) 1
в) 3
г) 5
д) 0
|
|
| 17.
| Обчислити вагу функції U=x+y+z+2, якщо задані ваги аргументів Px=Py=Pz=1.
| Р.1:П.10
|
|
| а) 1/5
б) 1/7
в) 1/2
г) 1/3
д) 0
|
|
| 18.
| Вимір з середньою квадратичною похибкою m1=3,0"; має вагу P1=25. Яка вага відповідає виміру з середньою квадратичною похибкою m2=5,0"?
| Р.1:П.8
|
|
| а) 9
б) 5
в) 3
г) 1
д) 0
|
|
| 19.
| Радіус кола виміряний з вагою  . Визначити вагу довжини кола.
| Р.1:П.10
|
|
| а) 0,5
б) 0,25
в) 0,75
г) 1,0
д) 0
|
|
| 20.
| Довжина кола виміряна з похибкою mD=6,28. Визначити середню квадратичну похибку радіуса кола.
| Р.1:П.6
|
|
| а) 5
б) 3
в) 1
г) 10
д) 0
|
|
| 21.
| Обчислити першу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
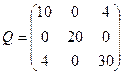
| Р.4:П.6
|
|
| а) 94
б) -22
в) -94
г) 22
д) 0
|
|
| 22.
| Обчислити другу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок 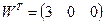 , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
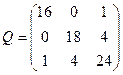
| Р.4:П.6
|
|
| а) -48
б) 3
в) -3
г) 0
д) 30
|
|
| 23.
| Обчислити третю корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -32
б) 32
в) -104
г) 104
д) 0
|
|
| 24.
| Обчислити першу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -44
б) 44
в) -48
г) 48
д) 0
|
|
| 25.
| Обчислити другу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок 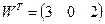 , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -38
б) 38
в) 21
г) -21
д) 0
|
|
| 26.
| Обчислити третю корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -70
б) -40
в) 40
г) 70
д) 0
|
|
| 27.
| Обчислити першу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
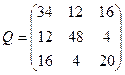
| Р.4:П.6
|
|
| а) -36
б) -12
в) 36
г) 12
д) 0
|
|
| 28.
| Обчислити другу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок  , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -55
б) 55
в) -83
г) 83
д) 0
|
|
| 29.
| Обчислити третю корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок 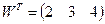 , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
| Р.4:П.6
|
|
| а) -16
б) -40
в) -80
г) -110
д) 0
|
|
| 30.
| Обчислити першу корелату для зрівноважування геодезичної мережі корелатним методом, якщо вектор нев’язок 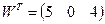 , а обернена матриця Q коефіцієнтів нормальних рівнянь корелат має вигляд:
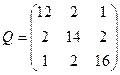
| Р.4:П.6
|
|
| а) 64
б) -64
в) 69
г) -69
д) 0
|
|
