Определение коэффициентов дискриминантной функции.
Рассмотрим случай для двух дискриминантных переменных:
f(x) = а1Х1 + а2Х2.
Функция f(X) называется канонической дискриминантной функцией, а величины x1 и x 2 – дискриминантными переменными. Дискриминантная функция может быть как линейной, так и нелинейной. Выбор вида этой функции зависит от геометрического расположения разделяемых классов в пространстве дискриминантных переменных. Коэффициенты дискриминантной функции (аi) определяются таким образом, чтобы Вектор коэффициентов дискриминантной функции определяется по формуле:
Полученные значения коэффициентов подставляют в формулу и для каждого объекта в обоих множествах вычисляют дискриминантные функции f(X), затем находят среднее значение для каждой группы ( Перед тем как приступить непосредственно к процедуре классификации, нужно определить границу, разделяющую два множества. Такой величиной может быть значение функции, равноудаленное от
Величина с называется константой дискриминации. Объекты, расположенные над разделяющей поверхностью f(x) = a1x1 + а2х2+…+ архр = с находятся ближе к центру множества М1, следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой поверхности, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами будет таким образом, то суммарная вероятность ошибочной классификации будет минимальной.
|

 (X)и
(X)и  (Х) как можно больше отличались между собой.
(Х) как можно больше отличались между собой.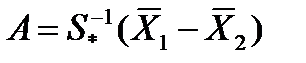
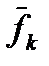 ). Таким образом, каждому i -му наблюдению, которое первоначально описывалось m -переменными, будет соответствовать одно значение дискриминантной функции, и размерность признакового пространства снижается.
). Таким образом, каждому i -му наблюдению, которое первоначально описывалось m -переменными, будет соответствовать одно значение дискриминантной функции, и размерность признакового пространства снижается. ,т.е.
,т.е. .
.


