Обратная задача теории погрешности.
Часто возникает обратная задача теории погрешностей: какой точности должны быть исходные данные, чтобы получить результат заданной точности? Для случая дифференцируемой функции одной переменной грубое решение обратной задачи тривиально: если
В качестве другого довольно естественного допущения можно принять равенство относительных погрешностей всех аргументов, т.е. считать При больших количествах однотипных вычислений вступают в силу вероятностные или статистические законы формирования погрешностей результатов действий. Например, методами теории вероятностей показывается, что математическое ожидание абсолютной погрешности суммы
Применение правила Чеботарева увеличивает точность оценивания по сравнению с классической теорией погрешностей. Прямое применение вероятностно-статистических оценок погрешностей также является достаточно сложным делом и вряд ли может быть рекомендовано при рядовых массовых вычислениях. Однако именно такие оценки подкрепляют практические правила работы с приближенными числами, составляющие основу так называемого технического подхода. Согласно принципу А. Н. Крылова, приближенное число должно записываться так, чтобы в нем все значащие цифры, кроме последней, были верными и лишь последняя была бы сомнительна, и притом в среднем [1] не более чем на одну единицу. Чтобы результаты арифметических действий, совершаемых над приближенными числами, записанными в соответствии с принципом А. Н. Крылова, также соответствовали этому принципу, нужно придерживаться следующих простых правил: 1) при сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим количеством десятичных знаков; 2) при умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр; 3) результаты промежуточных вычислений должны иметь один-два запасных знака (которые потом должны быть отброшены). Таким образом, при техническом подходе к учету погрешностей приближенных вычислений предполагается, что в самой записи приближенного числа содержится информация о его точности.
[1] «В среднем» здесь понимается в вероятностном смысле.
|
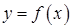, то 
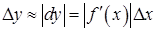, откуда 
. Для функции большего числа переменных обратная задача, вообще говоря, некорректна. Нужны дополнительные условия. Например, применяют принцип равных влияний, состоящий в предположении, что частные дифференциалы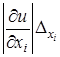 
в (4.1) одинаково влияют на погрешность значения функции; тогда
, откуда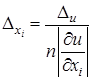 
(4.3)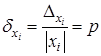
при всех 
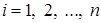. Тогда 
и, значит,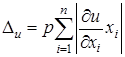 
. Из последнего равенства получаем величину 
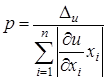(характеризующую относительный уровень точности задания аргументов), на основе которой за границы абсолютных погрешностей аргументов принимаем 
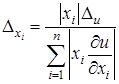. Имеются и другие, более сложные подходы к решению обратной задачи.
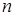слагаемых с одинаковым уровнем абсолютных погрешностей, при достаточно большом 
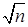. В частности, если 
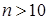и все слагаемые округлены до 
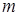-го десятичного разряда, то для подсчета абсолютной погрешности суммы 
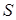применяют правило Чеботарева
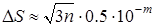(4.4)
