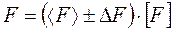ОБРАБОТКА РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ

Результат косвенного измерения определяется с помощью некоторой формулы, куда подставляют результаты прямых измерений. При этом должны быть известны средние значения и доверительные интервалы для результатов прямых измерений.

Представим формулу для расчёта в виде функции, где переменными являются результаты прямых измерений.

Например, объём шара:

,

площадь прямоугольника:

,

плотность массы:

,

объем параллелепипеда:

Формулы могут иметь более сложный вид, содержать степенные либо тригонометрические функции, иметь большое число переменных.

Рассмотрим в общем виде функцию двух переменных:

где x, y – результаты прямых измерений;

В теории измерений доказано, что среднее значение результата косвенных измерений вычисляется подстановкой в соответствующую формулу средних значений результатов прямых измерений:

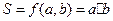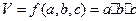
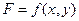
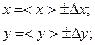
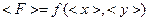
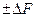Для расчёта доверительного интервала используется правило вычисления дифференциала функции. При этом учитывается физическое содержание (физическое понятие) дифференциала, а именно: дифференциал определяет область (интервал) существования значений данной функции в зависимости от области (интервала), в котором заданы переменные.

Итак, выполняя дифференцирование функции двух переменных, имеем:

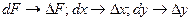Эта математическая формула преобразуется в теории измерений к другому виду, во-первых, заменой и, во-вторых, вычислением модуля значений величины 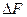, т.к. производные от функции могут иметь положительный и отрицательный знаки, но погрешности измерений не могут «компенсировать» друг друга, а должны только суммироваться. Применяя известное правило вычисления модуля, получим формулу:

В этой формуле под знаком корня «отброшены» удвоенные произведения как величины более высокого порядка малости. Положительное значение радикала определяет модуль значения - интервала, в котором существует найденное в эксперименте численное значение результата косвенных измерений. Окончательный результат имеет вид:

Следует помнить, что все значения для результатов прямых измерений должны вычисляться при одной и той же доверительной вероятности p. При этом же значении p будетопределен интервал .