Определение абсолютных и относительных погрешностей прямых измерений погрешность
При прямом измерении искомая величина определяется непосредственно путем отсчета по шкале измерительного прибора. Из приведенных выше рассуждений вытекает, что для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. Проводим измерение n раз. В результате получаем n значений величины: x1, x2, x3,... xn. (5.1.) Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Каждое прямое измерение содержит случайную ошибку, которую следует прибавить к результату измерения. От истинного значения результат измерения отличается на величину абсолютной погрешности с противоположным знаком:
где: Абсолютные погрешности могут принимать как положительные, так и отрицательные значения. Для того, чтобы при усреднении, абсолютная ошибка не уменьшалась, для вычислений используется ее модуль, который всегда положителен. Суммируя левую и правую часть равенств
Среднее арифметическое значение
При увеличении числа измерений до бесконечности среднее арифметическое значение стремиться к истинному значению измеряемой величины. При меньшем числе измерений истинное значение можно определить как:
где Соответственно формула (5.5) определяет среднеарифметическое значение абсолютной погрешности. Оценки результат измерений по формуле На практике при проведении ограниченного числа измерений мы не знаем точного значения дисперсии, а можем лишь оценить ее величину. Наилучшей оценкой среднего квадратичного отклонения s является Средней квадратичной ошибкой отдельного результата измерения называется величина:
Эта величина статистически стремится кsпри n ®¥. Таким образом, мы неизбежно заменяем величину s в доверительном интервале на ее приближенное значение nS. При этом необходимо помнить, что чем меньше число измерений, тем хуже это приближение. Так, теория показывает, что для корректного определения доверительного интервала с доверительной вероятностью w = 0,9 требуется не менее 40 измерений. Выше рассматривалась вероятность отклонения результата отдельного измерения от истинного значения величины x. Не менее важно знать, насколько может отклоняться от истинного значения среднее арифметическое результатов измерений. Это отклонение также характеризуется доверительным интервалом (<x> ± D x) w но таким, в котором с доверительной вероятностью w находится среднеарифметическое значение измеренной величины. Строго говоря, если величина x имеет нормальное распределение с математическим ожиданием m и дисперсиейs2, то и ее среднее значение <x>; имеет нормальное распределение с математическим ожиданием mи дисперсией s2/ n. Т.е. случайнаяпогрешность среднего арифметического меньше, чем погрешность единичного измерения. Если в качестве оценкиs используется средняя квадратичная погрешность nS, то для оценки отклонения среднего значения применяется средняя квадратичная погрешность среднего арифметического nS<x>:
Величина nS<x> статистически стремится к нулю при n ®¥. В теории ошибок доказывается, что при небольшом числе измерений (n < 30), которое реально имеет место в работах физического практикума, в доверительный интервал необходимо ввести коэффициент tw,n, называемый коэффициентом Стьюдента. Тогда доверительный интервал принимает вид: (< x > ± tw,n nS<x>) w. (5.9) Чем меньше число n проведенных измерений, тем больше среднее значение может отклониться от истинного. Значит, при одной и той же доверительной вероятности w коэффициент Стьюдента должен расти с уменьшением n, см. табл. 1. Таблица 1. Значения коэффициентов Стъюдента.
С ростом числа измерений среднеквадратичная ошибка среднеарифметического значения отклонения результата от истинного значения уменьшается, точность измерений возрастает, пропорционально корню квадратному из числа измерений. Это фундаментальный закон возрастания точности при росте числа измерений. Результат измерения принято записывать в виде:
где: 2
|

 ,.(5.2)
,.(5.2)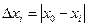 -абсолютная погрешность i –того измерения,
-абсолютная погрешность i –того измерения,  - истинное значение измеряемой величины.
- истинное значение измеряемой величины. а (5.2) почленно, получаем:
а (5.2) почленно, получаем: (5.3)
(5.3) результата измерений является основной числовой характеристикой центра группирования распределения случайных величин
результата измерений является основной числовой характеристикой центра группирования распределения случайных величин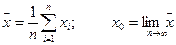 , (5.4)
, (5.4) ;
; 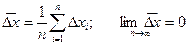
 (5.7)
(5.7) (5.8)
(5.8) n
w
n
w
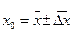 , (5.9)
, (5.9)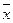 определяется по формуле (5.4), а
определяется по формуле (5.4), а  - по формуле (5.5) либо (5.9)
- по формуле (5.5) либо (5.9)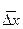 - принято называть доверительным интервалом. В соответствии с (5.9) истинное значение измеренной величины характеризуется среднеарифметическим значением серии измерений и лежит внутри доверительного интервала с вероятностью, зависящей от числа измерений либо выбранного для оценки границ интервала коэффициента Стьюдента.
- принято называть доверительным интервалом. В соответствии с (5.9) истинное значение измеренной величины характеризуется среднеарифметическим значением серии измерений и лежит внутри доверительного интервала с вероятностью, зависящей от числа измерений либо выбранного для оценки границ интервала коэффициента Стьюдента.


