Метод наименьших квадратов.

Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x. В результате измерений получается ряд значений:

x₁, x₂,..., x_i,,..., x_n;

y₁, y₂,..., y_i,,..., y_n.

По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. величина (y_i–ƒ(x_i))² была наименьшей.

На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда

Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением n = a + b/λ², то на графике строят зависимость n от λ^-2.

Задача состоит в том, чтобы по имеющемуся набору значений x_i, y_i найти наилучшие значения a и b.

Cоставим квадратичную форму φ;, равную сумме квадратов отклонений точек x_i, y_i от прямой

и найдем значения a и b, при которых φ имеет минимум

;

.

.

Совместное решение этих уравнений дает

.

Среднеквадратичные ошибки определения a и b равны

.
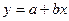
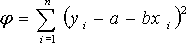
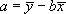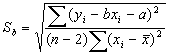