Ударный ток короткого замыкания
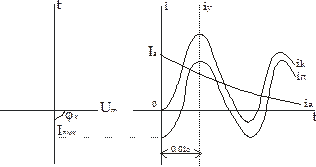
Ударным током короткого замыкания называют максимальное мгновенное значение полного тока при наиболее неблагоприятных условиях. Для электрических схем с преобладанием индуктивности таковые имеют место, если доаварийным режимом был холостой ход, а короткое замыкание происходит в момент прохождения напряжения через нуль (рисунок 3.3). При этом периодическая составляющая тока КЗ начинается с амплитудного значения. Согласно законам коммутации в первый момент КЗ начальное значение апериодической составляющей оказывается максимально возможным и равным амплитуде периодической составляющей тока КЗ Ia(0) = Inm
Рисунок 3.3. Ударный ток КЗ
Наибольшее мгновенное значение полного тока короткого замыкания –ударный ток возникает при первом наибольшем значении апериодической составляющей, совпадающей по знаку с периодической составляющей тока короткого замыкания. Этот момент наступает примерно через полпериода после появления короткого замыкания. При этом условии ударный ток I у = Iп m + Iп m e –0,01/Ta = Iп m (1 + e—0,01/Ta) = Iп m kу. Величину
Ударный коэффициент зависит от постоянной времени затухания апериодической составляющей Ta = xk / (314rk). При хк./rk ® 0 ky ® 1, а при хк./rk ® ¥ ky ® 2, т.е. значения ударного коэффициента изменяются в пределах 1<ку<2.
где I" - сверхпереходный ток КЗ (действующее значение периодической составляющей в первый момент КЗ).
|
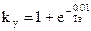называют ударным коэффициентом, характеризующим превышение ударного тока над амплитудой периодической составляющей тока КЗ
.
,
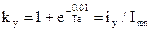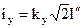