Применение системы относительных единиц
При решении задач о переходных процессах удобно использовать специальный метод предоставления информации – систему относительных единиц, которая дает универсальность записи математических уравнений и упрощает использование как конечных, так и промежуточных результатов. Относительным значением некоторой физической величины называется отношение этой физической величины к некоторой другой именованной величине, выбранной за базисную. Параметры различных элементов электроэнергетических систем, а также параметры режима (напряжение, ток, мощность и т. д.), как и другие физические величины, могут быть выражены как в системе именованных, так ив системе относительных единиц, т.е. в долях от определенных значений этих же величин, принятых за единицу измерения. При этом точность получаемых результатов расчетов не зависит от используемой системы единиц измерения. Применение системы относительных единиц часто существенно упрощает расчетные выражения, описывающие процессы в различных элементах электроэнергетической системы, облегчает контроль расчетных данных и сопоставление результатов расчетов для установок различной мощности, поскольку для таких установок относительные значения расчетных величин часто имеют одинаковый порядок. Чтобы получить относительные значения различных физических величин, необходимо предварительно выбрать значения соответствующих величин, принимаемые за базисные, т.е. в качестве единиц измерения. В частности, чтобы выразить параметры различных элементов схемы замещения электрической цепи и параметры режима в системе относительных единиц, необходимо иметь четыре базисные единицы: базисное напряжение
и формулы, выражающей закон Ома: При выбранных базисных единицах относительные значения ЭДС, напряжения, тока, мощности и сопротивления определяют путем деления значения соответствующей величины в именованных единицах на базисную единицу той же размерности:
причем выбранные базисные единицы служат единицами измерения как полных величин, так и их составляющих. Иногда относительные значения величин выражают в процентах от соответствующих базисных единиц, для чего эти значения умножают на 100. Очевидно, что относительные значения фазного и линейного напряжений одинаковы. Также одинаковы относительные значения фазной мощности и мощности трех фаз. Часто для определения относительного сопротивления вместо используют другие соотношения:
Из формулы следует, что сопротивление в относительных единицах численно равно относительному падению напряжения в соответствующем элементе от базисного тока. Часто параметры элементов электроэнергетических систем, вводимых в расчетную схему, заданы не в именованных единицах, а в процентах или относительных единицах при номинальных условиях. Это означает, что при выражении их в процентах или в относительных единицах в качестве базисных единиц были приняты номинальное напряжение Например, обычно активное и индуктивное сопротивления воздушных и кабельных линий задают в Омах на единицу длины (километр), индуктивное сопротивление реакторов - в Омах (до недавнего времени – в процентах), полное сопротивление трансформаторов (оно численно равно напряжению короткого замыкания) - в процентах, а индуктивное сопротивление генераторов и синхронных компенсаторов - в относительных единицах при номинальных условиях. Для расчетов различных режимов электроэнергетических систем и токов КЗ прежде всего необходимо привести ЭДС и сопротивления всех элементов исходной расчетной схемы к одним базисным условиям.
Таблица 4.2. Формулы для расчета в относительных единицах
«Преобразование схем замещения»
Схемы замещения путём преобразований упрощают и находят эквивалентную ЭДС и эквивалентное сопротивление относительно места повреждения. Для преобразования схем используют известные способы: последовательное и параллельное сложение сопротивлений и ЭДС, преобразование треугольника в звезду или обратно, многолучевой звезды в полный многоугольник с диагоналями и так далее (смотри таблицу). При выполнении преобразований полезно использовать особые свойства схем, например, если схема симметрична относительно точки короткого замыкания, то потенциалы некоторых точек окажутся одинаковыми и их можно соединить между собой. Для расчета режимов при известных ЭДС применяют три метода: 1. эквивалентирование схемы замещения; 2. применение метода наложения; 3. расчет по уравнениям узловых напряжений; Рассмотрим первый метод. Согласно принципу наложения действительный режим можно рассматривать как результат наложения ряда условных режимов, каждый из которых определяется в предположении, что в схеме приложена только одна ЭДС. При этом сами генерирующие ветви, ЭДС которых принимаются равными нулю, должны быть сохранены в схеме своими сопротивлениями. При аналитическом решении задачи метод наложения становится весьма громоздким, если схема содержит большое число ЭДС. Если схема замещения не содержит замкнутых контуров и в ней имеется один или несколько источников ЭДС, то ее необходимо привести к простейшему виду путем элементарных преобразований как в обычных расчетах линейных электрических цепей. К ним относятся, например: замена нескольких генерирующих ветвей, присоединенных к общему узлу, одной эквивалентной; преобразования треугольника в звезду и обратно и т.д. Эквивалентная замена генераторных ветвей одним эквивалентным генератором возможна если: 1. Генераторы, питающие точку КЗ однотипные (турбогенераторы или гидрогенераторы). 2. Генераторы, питающие точку КЗ соизмеримой мощности и имеют соизмеримую удаленность от точки КЗ. Определение взаимных сопротивлений например, между источником и точкой КЗ при преобразовании схемы к радиальному (лучевому) виду (рисунок 4.1).
При преобразованиях схем в ходе выполнения расчетов нужно учитывать некоторые специфические особенности: 1. Первоочередной задачей расчета тока КЗ является определение тока непосредственно в аварийной ветви или в месте КЗ.
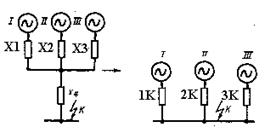
2. Когда КЗ находится в узле с несколькими сходящимися в нем ветвями, этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же КЗ. Далее полученную схему нетрудно преобразовать относительно любой из точек КЗ, учитывая другие ветви с КЗ как нагрузочные ветви с ЭДС равными нулю (рисунок 4.3).
Определенные трудности в упрощении схем возникают, когда точка КЗ находится в одном из узлов многоугольника, к другим узлам которого присоединены генерирующие ветви (рисунок 4.4).
Рис.4.4.Преобразование схемы Если точка КЗ делит схему на две симметричные части, например точки К1, К2, то при одинаковых характеристиках генераторов G1, G3 и трансформаторов узлы а и b схемы будут иметь одинаковые потенциалы, вследствие чего их ожно совместить: ветви генераторов G1 и G3 объединяют, представляя их эквивалентной машиной с S = 2Sном. В результате получится схема ” в ”. В этой схеме Преобразуем схему, приведенную на рис.2.5. Если генераторы G1 и G2 имеют одинаковые ЭДС, то их можно объединить в эквивалентный генератор с мощностью S = 2Sном.
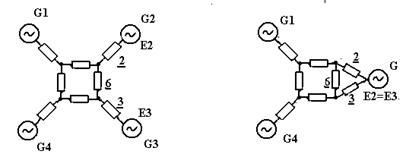
Далее преобразовывая, получим: Если схема имеет одинаковые ЭДС, то в некоторых случаях упрощение схемы достигается объединением источников. Например, если схема на рис.2.6,а имеет одинаковые ЭДС Е2 и Е3, то объединяя эти ЭДС и преобразуя полученный треугольник 2-3-6 в эквивалентную звезду, получим схему (рисунок 4.6.б).
А б Рисунок 4.6. Преобразование схемы
Следует отметить, что трудность преобразования схем замещения в значительной степени определяется выбранным порядком выполнения операций по упрощению схемы. Поэтому при преобразовании схем следует придерживаться такого порядка расчётов и записи результатов, который обеспечивает проверку полученных результатов. После получения простейшей схемы содержащей точку КЗ и эквивалентную ЭДС за эквивалентным сопротивлением приступают к расчёту тока КЗ. Токи и напряжения в других ветвях схемы (если в этом есть необходимость) определяют, совершая обратный переход от простейшей схемы к всё более сложным, вплоть до исходной.
|

 , базисный ток
, базисный ток 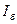 , базисную мощность (трехфазной системы)
, базисную мощность (трехфазной системы) 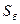 и базисное сопротивление
и базисное сопротивление  . Две из них выбирают произвольно, а две другие определяют из соотношения для мощности трехфазной системы
. Две из них выбирают произвольно, а две другие определяют из соотношения для мощности трехфазной системы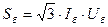
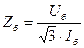
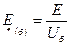
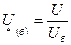
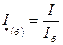
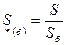
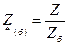
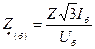

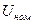 и номинальный ток
и номинальный ток 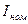 или номинальная мощность
или номинальная мощность 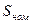 .
.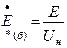
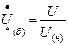


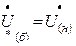

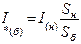


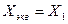 êê
êê  êê
êê 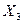 ,
,

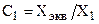 ,
,  ,
, 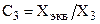 Проверка: С1 + С2 + С3 = 1.
Проверка: С1 + С2 + С3 = 1.
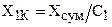 ,
,  ,
, 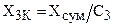 .
.



 êê
êê  ,
, 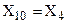 êê
êê 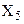 ,
,  .
.
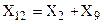 ,
, 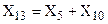 . Полученный треугольник Х3, Х12, Х13, преобразуется в звезду Х14, Х15, Х16 (рис.2.5,в). Последовательно сложив сопротивления
. Полученный треугольник Х3, Х12, Х13, преобразуется в звезду Х14, Х15, Х16 (рис.2.5,в). Последовательно сложив сопротивления 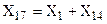 и
и 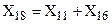 , получим схему рис. 2.5,г.
, получим схему рис. 2.5,г.