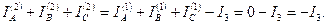Метод симметричных составляющих
Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковыхусловиях работы фаз. Сформулируем основные положения метода симметричных составляющих. 1. Любую несимметричную систему токов можно разложить на три симметричные, называемые системами прямой, обратной нулевой последовательностей. Эти системы получили название «симметричные составляющие». Предполагается, что они одновременно циркулируют в рассматриваемой сети в несимметричном режиме. 2. Симметричная система токов прямой последовательности (рисунок 5.1, а) представляет собой три одинаковых по величине вектора, расположенных под углом 120°, вращающихся против часовой стрелки так, что соблюдается нормальное чередование фаз: А - В - С. Соотношения между фазными значениями устанавливаются с помощью оператора Этот вектор единичной длины имеет аргумент, равный 120°. Если некоторый вектор, например I А1, умножить на а, то это означает повернуть I А1 на 120° против часовой стрелки. С помощью вектора а можно выразить токи фаз В и С через ток фазы А: І B1 = а 2 І A1 І C1 = аІ A1 3. Симметричная система токов обратной последовательности (рисунок 5.1, б) представляет собой три одинаковых по величине вектора, расположенных под углом 120° и вращающихся против часовой стрелки так, что соблюдается обратное чередование фаз: А - С - В. При этом токи фаз В и С связаны с током фазы А следующим образом: І B2 = аІ A2 І C2 = а 2 І A2
Рисунок 5.1. Система токов прямой (а), обратной (б) и нулевой (в) последовательностей
4. Симметричная система токов нулевой последовательности (рисунок 5.1, в) существенно отличается от прямой и обратной. Она представляет собой систему трех переменных токов, совпадающих по фазе и имеющих одинаковую амплитуду. Эти токи являются, по существу, разветвлением однофазного тока, для которого три провода трехфазной цепи составляют один прямой провод, а обратным служит земля или четвертый (нулевой) провод. Появление токов нулевой последовательности в сети означает возникновение в ней несимметричного замыкания на землю. Рассматриваемая несимметричная система токов допускает только одно разложение на симметричные составляющие. Действительно, представив ток каждой фазы через его симметричные составляющие, получим I A = І A1 + I A2 + I A0, I B = a 2 І A1 + aI A2 + I A0, I C = aІ A1 + a2I A2 + I A0,
Если I A ,I B, I C заданы, то искомыми являются три величины I A1 ,I B2, I C0. Они определяются тремя линейными уравнениями, которые допускают только одно решение:
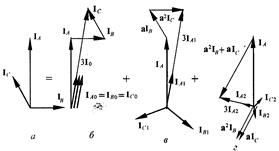
Все соотношения для симметричных составляющих токов справедливы и для напряжений. Рассмотрим разложение на составляющие несимметричной системы токов (рис 4.3, а). С помощью геометрических построений, соответствующих выражениям и найдем ток нулевой, прямой и обратной последовательностей (рисунок 5.2, б-г). Если сложить симметричные составляющие в соответствии с выражениями, то получим исходную систему.
Рис 5.2. Разложение несимметричной системы токов на симметричные сотавляющие
5. В трехфазной цепи в месте КЗ наряду с напряжениями прямой последовательности возникают напряжения обратной и нулевой последовательностей. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей. Для иллюстрации этого положения рассмотрим схему электрической системы, показанную на рисунок 5.4. За положительное направление токов примем направление слева направо и допустим, что картина распределения имеет вид, показанный на рисунке. Тогда для участка 1 для участка 2 для участка 3
Из этих соотношении видно, что ток нулевой последовательности, определяемый по выражению, циркулирует только на участке 2. Для участков 1и 2 можно записать следующие соотношения: где I 3 - ток в земле. Отсюда, В симметричных электрических системах токи и напряжения схем отдельных последовательностей могут рассматриваться независимо друг от друга и быть связаны между собой законами Ома и Кирхгофа. Если какой-либо элемент цепи симметричен и при протекании по нему токов I1, I2, I0,обладает некоторыми сопротивлениями Z1, Z2, Z0,симметричные составляющие падении напряжения в этом элементе будут равны ∆Z 1 = I 1 Z 1, ∆Z 2 = I 2 Z 2, ∆Z 0 = I 0 Z 0, Комплексная форма уравнений справедлива ни только для Стационарного режима, но и для переходного, так как токи и напряжения при переходном процессе можно представить проекциями вращающихся векторов на соответствующую ось. При этом Дифференциальным уравнениям, связывающим комплексные значения, отвечают операторные уравнения, которые при нулевых начальных условиях по своей структуре аналогичны уравнениям стационарного режима, записанным в комплексной форме. Уравнения второго закона Кирхгофа для любого КЗ каждой последовательности могут быть записаны в виде U K1 = E Σ - Z 1Σ I K1, U K2 = 0 – Z 2Σ I K2, U K0 = 0 – Z 0Σ I K0: где U K1, U K2, U K0, I K1, I K2, I K0- симметричные составляющие Напряжения и тока в месте КЗ; E Σ - результирующая ЭДС относительно точки КЗ; Z 1Σ, Z 2Σ, Z 0Σ - результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ. Запись уравнений второго закона Кирхгофа вызывает необходимость сформулировать следующее положение метода симметричных составляющих. Элементы трехфазной сети для токов прямой, обратной и нулевой последовательностей имеют неодинаковые сопротивления. ЭДС генераторов симметричны, т.е. не содержат обратной и нулевой составляющих. Отсюда следует, что: а) в электрических системах существуют только ЭДС прямой последовательности; б) токи обратной и нулевой последовательностей определяются только напряжениями в точке КЗ. Между системами трех симметричных составляющих всегда существует связь, задаваемая условиями короткого замыкания. Эта связь легко устанавливается путем перевода граничных условий короткого замыкания, заданных через действительные токи и напряжения, в условия, заданные через симметричные составляющие.
|

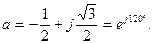

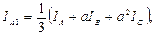

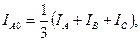
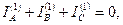

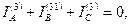

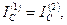
 или
или