Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наибольшего значения 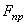 . При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и
. При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и 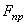 , где
, где  . Затем составляют обычные условия равновесия статики, подставляют в них вместо
. Затем составляют обычные условия равновесия статики, подставляют в них вместо 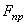 величину
величину 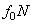 и, решая полученные уравнения, определяют искомые величины.
и, решая полученные уравнения, определяют искомые величины.
Пример 1. Рассмотрим тело, имеющее вертикальную плоскость симметрии (рис.28). Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2 a.
К телу в точке С, лежащей на оси симметрии, приложена вертикальная сила  и в точке А, лежащей на расстоянии
и в точке А, лежащей на расстоянии 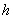 от основания, горизонтальная сила
от основания, горизонтальная сила  . Реакция плоскости основания (реакция связи) приводится к нормальной реакции
. Реакция плоскости основания (реакция связи) приводится к нормальной реакции 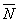 и силе трения
и силе трения 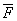 . Линия действия силы
. Линия действия силы 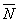 неизвестна. Расстояние от точки С до линии действия силы
неизвестна. Расстояние от точки С до линии действия силы 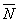 обозначим x (
обозначим x (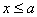 ).
).
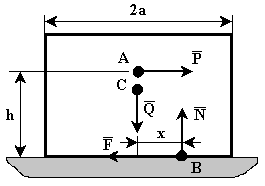
Рис.28
Составим три уравнения равновесия:
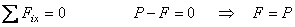
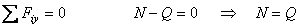
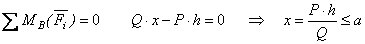
Согласно закону Кулона  , т.е.
, т.е.  . (1)
. (1)
Так как  , то
, то  (2)
(2)
Проанализируем полученные результаты:
Будем увеличивать силу  .
.
Если  , то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.
, то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.
Если 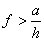 , то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины
, то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины  , условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).
, условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).
Пример 2. На какое максимальное расстояние а может подняться человек по лестнице, приставленной к стене (рис.29)? Если вес человека – Р, коэффициент трения скольжения между лестницей и стеной –  , между лестницей и полом –
, между лестницей и полом – 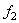 .
.
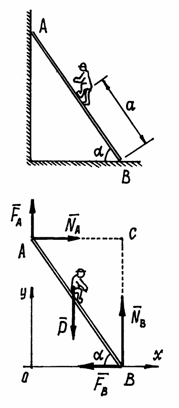
Рис.29
Рассматриваем равновесие лестницы с человеком. Показываем силу 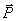 , нормальные реакции
, нормальные реакции 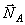 и
и  и добавляем силы трения:
и добавляем силы трения: 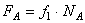 и
и  . Полагаем, что человек находится на расстоянии
. Полагаем, что человек находится на расстоянии  , при большем значении которого начнётся движение лестницы. Составляем уравнения равновесия.
, при большем значении которого начнётся движение лестницы. Составляем уравнения равновесия.
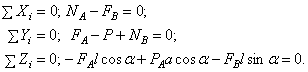
Подставив значения сил трения и решив систему уравнений, получим
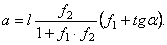
Теперь можно определить и угол под которым надо поставить лестницу, чтоб добраться до стены. Полагая 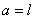 , получим, после преобразований,
, получим, после преобразований, 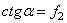 и
и 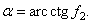
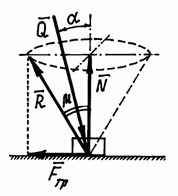
Рис.30
Заметим, что если равнодействующая  всех активных сил (всех кроме реакций) направлена под углом
всех активных сил (всех кроме реакций) направлена под углом  (рис.30), то нормальная реакция
(рис.30), то нормальная реакция 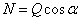 , а сила трения
, а сила трения 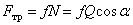 . Для того, чтобы началось скольжение должно выполнятся условие
. Для того, чтобы началось скольжение должно выполнятся условие 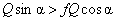 . или
. или  . И так как
. И так как 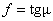 , то
, то  . Значит угол
. Значит угол  должен быть больше угла
должен быть больше угла 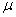 . Следовательно, если сила
. Следовательно, если сила  действует внутри угла или конуса трения (
действует внутри угла или конуса трения (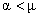 ), то как бы не была велика эта сила, скольжение тела не произойдёт. Такое условие называется условием заклинивания, самоторможения.
), то как бы не была велика эта сила, скольжение тела не произойдёт. Такое условие называется условием заклинивания, самоторможения.
Мы рассмотрели скольжение твёрдых тел по поверхности. Но нередко встречается скольжение гибких тел по неплоской поверхности. Например, нежелательное проскальзывание в ременной передаче ремня по шкиву, или троса, каната, намотанного на неподвижный цилиндр.
Пример 3. Пусть имеется нить, перекинутая через неподвижную цилиндрическую поверхность (рис.31). За счёт сил трения натяжение левого и правого концов этой нити будут различными.

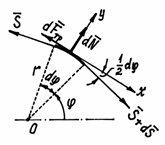
Рис.31 Рис.32
Предположим, что нормальная реакция и сила трения распределяются равномерно по дуге контакта нити на цилиндре. Рассмотрим равновесие участка нити длиной  . (рис.32). На левом конце этого участка натяжение
. (рис.32). На левом конце этого участка натяжение 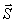 , на правом
, на правом 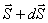 . Составляем уравнения равновесия, проектируя силы на оси:
. Составляем уравнения равновесия, проектируя силы на оси:

Так как угол  - малая величина, то полагаем
- малая величина, то полагаем 
 С учётом этого из уравнений находим
С учётом этого из уравнений находим 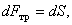
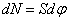 и, так как
и, так как  , имеем
, имеем 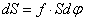 или
или  Интегрируя, получим
Интегрируя, получим  . Или
. Или
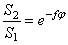 .
.
Этот результат называется формулой Эйлера.
Например, если нить перекинута через неподвижный шкив и  , а коэффициент трения
, а коэффициент трения  , то отношение натяжений
, то отношение натяжений 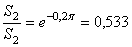 . А, обернув цилиндр один раз (
. А, обернув цилиндр один раз ( ),
), 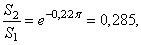 то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.
то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.

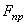 . При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и
. При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и  . Затем составляют обычные условия равновесия статики, подставляют в них вместо
. Затем составляют обычные условия равновесия статики, подставляют в них вместо 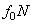 и, решая полученные уравнения, определяют искомые величины.
и, решая полученные уравнения, определяют искомые величины. и в точке А, лежащей на расстоянии
и в точке А, лежащей на расстоянии 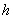 от основания, горизонтальная сила
от основания, горизонтальная сила  . Реакция плоскости основания (реакция связи) приводится к нормальной реакции
. Реакция плоскости основания (реакция связи) приводится к нормальной реакции 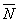 и силе трения
и силе трения 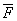 . Линия действия силы
. Линия действия силы 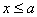 ).
).
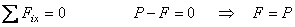
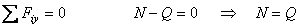
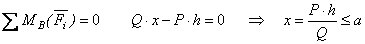
 , т.е.
, т.е.  . (1)
. (1) , то
, то  (2)
(2) .
. , то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.
, то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.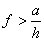 , то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины
, то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины  , условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).
, условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет). , между лестницей и полом –
, между лестницей и полом – 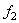 .
.
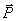 , нормальные реакции
, нормальные реакции 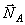 и
и  и добавляем силы трения:
и добавляем силы трения: 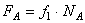 и
и  . Полагаем, что человек находится на расстоянии
. Полагаем, что человек находится на расстоянии  , при большем значении которого начнётся движение лестницы. Составляем уравнения равновесия.
, при большем значении которого начнётся движение лестницы. Составляем уравнения равновесия.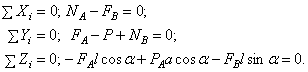
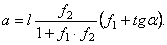
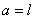 , получим, после преобразований,
, получим, после преобразований, 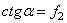 и
и 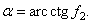

 всех активных сил (всех кроме реакций) направлена под углом
всех активных сил (всех кроме реакций) направлена под углом  (рис.30), то нормальная реакция
(рис.30), то нормальная реакция 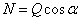 , а сила трения
, а сила трения 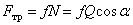 . Для того, чтобы началось скольжение должно выполнятся условие
. Для того, чтобы началось скольжение должно выполнятся условие 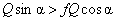 . или
. или  . И так как
. И так как 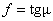 , то
, то  . Значит угол
. Значит угол 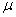 . Следовательно, если сила
. Следовательно, если сила 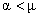 ), то как бы не была велика эта сила, скольжение тела не произойдёт. Такое условие называется условием заклинивания, самоторможения.
), то как бы не была велика эта сила, скольжение тела не произойдёт. Такое условие называется условием заклинивания, самоторможения.

 . (рис.32). На левом конце этого участка натяжение
. (рис.32). На левом конце этого участка натяжение 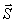 , на правом
, на правом 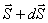 . Составляем уравнения равновесия, проектируя силы на оси:
. Составляем уравнения равновесия, проектируя силы на оси:
 - малая величина, то полагаем
- малая величина, то полагаем 
 С учётом этого из уравнений находим
С учётом этого из уравнений находим 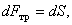
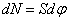 и, так как
и, так как  , имеем
, имеем 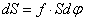 или
или  Интегрируя, получим
Интегрируя, получим  . Или
. Или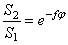 .
. , а коэффициент трения
, а коэффициент трения  , то отношение натяжений
, то отношение натяжений 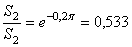 . А, обернув цилиндр один раз (
. А, обернув цилиндр один раз ( ),
), 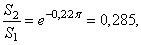 то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.
то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.


