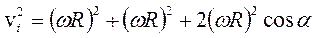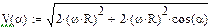Движение в потенциальном поле сил
Потенциальная энергия является функцией координат Перемещение Это можно переписать После этого записать вектор силы через градиент потенциальной энергии
Где векторный оператор набла связывает вектор силы и потенциальную энергию
Закон Ньютона примет вид
Пример.
Смысл градиента станет нагляднее и яснее, если ввести понятие эквипотенциальной поверхности - поверхности, во всех точках которой потенциальная энергия W имеет одно и то же значение. Ясно, что каждому значению W соответствует своя эквипотенциальная поверхность. Проекция вектора
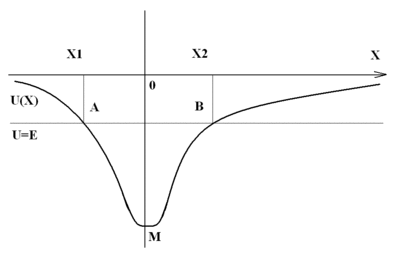
Потенциальная яма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.
Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону.
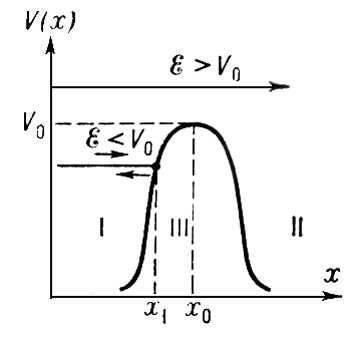
Потенциальный барьер
Для одномерных полей: Если задан график силы, то потенциальная энергия находится как интеграл от силы со знаком минус
Если задан график потенциальной энергии, то зависимость силы от координаты находится через производную со знаком минус
Пример: найти период движения частицы массой m с полной энергией Е 0 для заданной Выразим время как функцию от энергии Замена переменной
Скорость i -ой точки Скорость относительно ЦМ
|

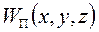 и может быть определена только в поле консервативных сил так что
и может быть определена только в поле консервативных сил так что  .
. . Соответственно изменение потенциальной энергии по каждому направлению
. Соответственно изменение потенциальной энергии по каждому направлению 


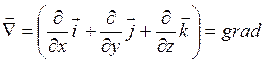
 .
.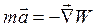 ;
;  .
.  .
.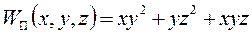 . Найти вектор силы.
. Найти вектор силы.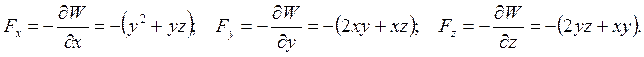
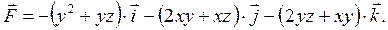
 на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор
на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор  в сторону уменьшения W, тогда D W < 0, и,
в сторону уменьшения W, тогда D W < 0, и,  т.е. вектор силы
т.е. вектор силы 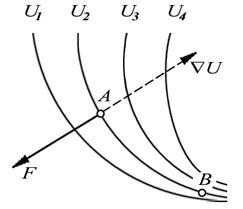
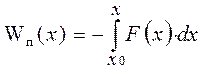
 .
. . Из закона сохранения энергии
. Из закона сохранения энергии  или
или  .
. и проинтегрируем от 0 до A.
и проинтегрируем от 0 до A.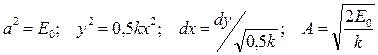 .
. это время составляет четвертую часть периода, значит период движения частицы в параболической потенциальной яме
это время составляет четвертую часть периода, значит период движения частицы в параболической потенциальной яме .
. Кинематика вращательно-поступательного движения
Кинематика вращательно-поступательного движения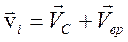
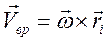

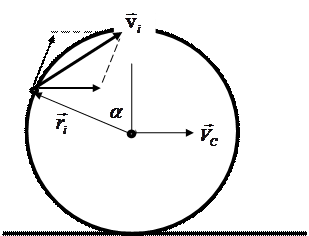 Точка находится на ободе колеса:
Точка находится на ободе колеса: ;
; 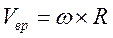 ;
; 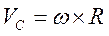 ;
;