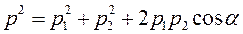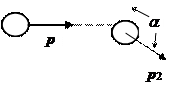Теорема о движении центра масс
Следствия из законов сохранения Теорема о движении центра масс
В некоторых случаях при исследовании движения механической системы можно ограничиться изучением движения ее центра масс.
Теорема. Центр масс механической системы движется как материальная точка с массой, равной массе всей системы, к которой приложена сила, равная главному вектору внешних сил 1) Внутренние силы не влияют на движение центра масс. 2) Если главный вектор внешних сил равен нулю, то центр масс движется равномерно и прямолинейно или находится в покое. 3) Если проекция главного вектора внешних сил на какую-либо из осей равна нулю, то по отношению к этой оси центр масс движется равномерно или соответствующая координата центра масс постоянна.
Теорема о движении центра масс позволяет, в частности, записать дифференциальные уравнения поступательного движения твердого тела. Примеры: снаряд, летящий по параболе, разрывается на много осколков. Так как сила взрыва – это внутренняя сила, то центр масс осколков продолжает двигаться по параболе, а суммарный импульс осколков в момент разрыва равен импульсу снаряда до разрыва согласно закону сохранения импульса.
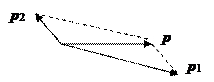
Диаграмма импульсов
Соударение бильярдных шаров:
  ; 
|
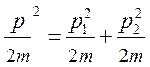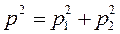
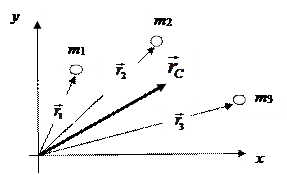Центром масс механической системы называется точка, положение которой определяется радиус-вектором: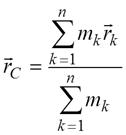
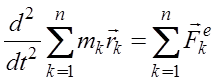Þ 
Þ 
Þ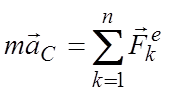 
.
, 
, 
.
; 
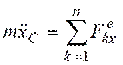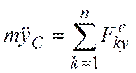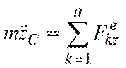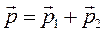