Формула трапеций
Отчет по лабораторной работе №6 по дисциплине «Вычислительная математика» Вариант №24 Выполнил: студент группы АСП-02-10 Фомин И.А.
Проверил: Рябов Л.П.
Москва, 2012г. Задание. Вычислить по формуле трапеций и по формуле Симпсона определённый интеграл:
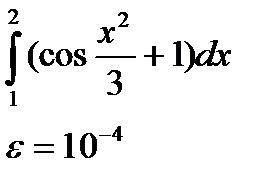
I. Методы решения: Формула трапеций Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций. В основе формулы трапеций лежит разбиение отрезка, содержащего n узлов на n+1 трапецию. Отдельно вычисляется площадь каждой отдельной трапеции, затем найденные площади суммируются. При увеличении числа трапеций полученная площадь стремится к площади фигуры под линией графика подынтегральной функции. Точность вычисления интеграла возрастает с увеличением n. В общем виде формула трапеций имеет вид:
R – величина погрешности. Rn = R1 + R2 + … + Rn – сумма погрешностей на отдельных площадках (трапециях). При увеличении количества площадок, точность вычисления интеграла увеличивается, и величина погрешности стремится к 0.
|

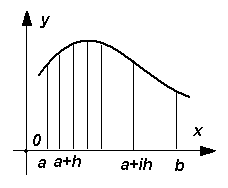

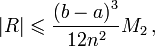 где
где