Определение. Пусть  – произвольный вектор,
– произвольный вектор,  – произвольная система векторов. Если выполняется равенство
– произвольная система векторов. Если выполняется равенство
 , (1)
, (1)
то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов
представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора
является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису
по базису  . Коэффициенты линейной комбинации
. Коэффициенты линейной комбинации  называются в этом случае координатами вектора
называются в этом случае координатами вектора  относительно базиса
относительно базиса  .
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и  – базис
– базис  . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то  . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 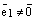 , то найдется (существует) такое число
, то найдется (существует) такое число  , что
, что 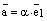 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора  по базису
по базису  векторного пространства
векторного пространства  .
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису  векторного пространства
векторного пространства  :
:
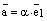 и
и 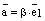 , где
, где 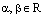 . Тогда
. Тогда  и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем:
 .
.
Так как 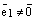 , то из последнего равенства следует, что
, то из последнего равенства следует, что  , ч.т.д.
, ч.т.д.
2) Пусть теперь Р произвольная плоскость и 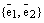 – базис
– базис  . Пусть
. Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую  , на которой лежит вектор
, на которой лежит вектор  , прямую
, прямую  , на которой лежит вектор
, на которой лежит вектор 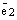 . Через конец вектора
. Через конец вектора  проведем прямую параллельную вектору
проведем прямую параллельную вектору  и прямую параллельную вектору
и прямую параллельную вектору 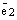 . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма
. Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма 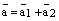 , и
, и  ,
, 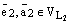 ,
,  – базис
– базис  ,
,  – базис
– базис  .
.
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа  , что
, что
 и
и  . Отсюда получаем:
. Отсюда получаем:
 и возможность разложения по базису доказана.
и возможность разложения по базису доказана.
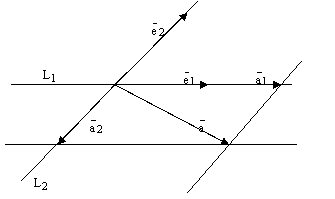
рис.3.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису 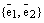 векторного пространства
векторного пространства  :
: 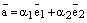 и
и 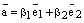 . Получаем равенство
. Получаем равенство
 , откуда следует
, откуда следует  . Если
. Если  , то
, то 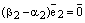 , а т.к.
, а т.к.  , то
, то  и коэффициенты разложения равны:
и коэффициенты разложения равны:  ,
,  . Пусть теперь
. Пусть теперь  . Тогда
. Тогда  , где
, где  . По теореме о коллинеарности двух векторов отсюда следует, что
. По теореме о коллинеарности двух векторов отсюда следует, что  . Получили противоречие условию теоремы. Следовательно,
. Получили противоречие условию теоремы. Следовательно,  и
и  , ч.т.д.
, ч.т.д.
3) Пусть  – базис
– базис 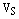 и пусть
и пусть 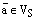 произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора 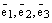 и вектор
и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы 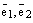 , плоскость
, плоскость  и плоскость
и плоскость  ; далее через конец вектора
; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
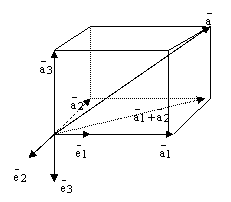
рис.4.
По правилу сложения векторов получаем равенство:
 . (1)
. (1)
По построению  . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число
. Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число  , такое что
, такое что  . Аналогично,
. Аналогично,  и
и  , где
, где  . Теперь, подставляя эти равенства в (1), получаем:
. Теперь, подставляя эти равенства в (1), получаем:
 (2)
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису  :
:
 и
и  . Тогда
. Тогда
 . (3)
. (3)
Заметим, что по условию векторы  некомпланарные, следовательно, они попарно неколлинеарные.
некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая:  или
или  .
.
а) Пусть  , тогда из равенства (3) следует:
, тогда из равенства (3) следует:
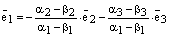 . (4)
. (4)
Из равенства (4) следует, что вектор  раскладывается по базису
раскладывается по базису 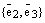 , т.е. вектор
, т.е. вектор  лежит в плоскости векторов
лежит в плоскости векторов 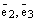 и, следовательно, векторы
и, следовательно, векторы 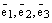 компланарные, что противоречит условию.
компланарные, что противоречит условию.
б) Остается случай  , т.е.
, т.е. 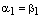 . Тогда из равенства (3) получаем
. Тогда из равенства (3) получаем 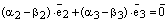 или
или
 . (5)
. (5)
Так как 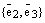 – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что
– базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что  и
и  , ч.т.д.
, ч.т.д.
Теорема доказана.

 – произвольный вектор,
– произвольный вектор,  – произвольная система векторов. Если выполняется равенство
– произвольная система векторов. Если выполняется равенство , (1)
, (1) называются в этом случае координатами вектора
называются в этом случае координатами вектора  – базис
– базис  . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то  . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 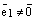 , то найдется (существует) такое число
, то найдется (существует) такое число  , что
, что 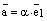 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора 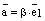 , где
, где 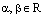 . Тогда
. Тогда  и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем: .
. , ч.т.д.
, ч.т.д. – базис
– базис  . Пусть
. Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую  , на которой лежит вектор
, на которой лежит вектор  , прямую
, прямую  , на которой лежит вектор
, на которой лежит вектор  . Через конец вектора
. Через конец вектора 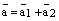 , и
, и  ,
, 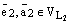 ,
,  – базис
– базис  , что
, что и
и  . Отсюда получаем:
. Отсюда получаем: и возможность разложения по базису доказана.
и возможность разложения по базису доказана.
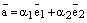 и
и 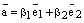 . Получаем равенство
. Получаем равенство , откуда следует
, откуда следует  . Если
. Если  , то
, то 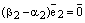 , а т.к.
, а т.к.  , то
, то  и коэффициенты разложения равны:
и коэффициенты разложения равны:  ,
,  . Пусть теперь
. Пусть теперь  . Тогда
. Тогда  , где
, где  . По теореме о коллинеарности двух векторов отсюда следует, что
. По теореме о коллинеарности двух векторов отсюда следует, что  . Получили противоречие условию теоремы. Следовательно,
. Получили противоречие условию теоремы. Следовательно,  – базис
– базис 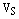 и пусть
и пусть 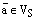 произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения.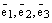 и вектор
и вектор 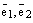 , плоскость
, плоскость  и плоскость
и плоскость 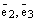 ; далее через конец вектора
; далее через конец вектора 
 . (1)
. (1) . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число
. Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число  , такое что
, такое что  . Аналогично,
. Аналогично,  , где
, где  . Теперь, подставляя эти равенства в (1), получаем:
. Теперь, подставляя эти равенства в (1), получаем: (2)
(2) . Тогда
. Тогда . (3)
. (3)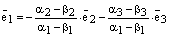 . (4)
. (4)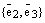 , т.е. вектор
, т.е. вектор 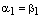 . Тогда из равенства (3) получаем
. Тогда из равенства (3) получаем 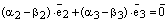 или
или . (5)
. (5) , ч.т.д.
, ч.т.д.


