Дискретизация непрерывных изображенийДискретизация – это преобразование непрерывного сигнала в последовательность чисел (отсчетов), то есть представление этого сигнала по какому-либо конечномерному базису. Это представление состоит в проектировании сигнала на данный базис. Наиболее удобным с точки зрения организации обработки и естественным способом дискретизации является представление сигналов в виде выборки их значений (отсчетов) в отдельных, регулярно расположенных точках. Такой способ называют растрированием, а последовательность узлов, в которых берутся отсчеты - растром. Интервал, через который берутся значения непрерывного сигнала называется шагом дискретизации. Обратная шагу величина называется частотой дискретизации, Наиболее употребительной является периодическая дискретизация, в частности, дискретизация с прямоугольным растром.
Пусть xH(t1,t2) - непрерывное изображение, а x(i 1, i2) - соответствующее ему дискретное, полученное из непрерывного путем прямоугольной дискретизации. Рис. 4.1 иллюстрирует расположение отсчетов на плоскости (t1,t2) при прямоугольной дискретизации.
Существенный вопрос, возникающий в ходе дискретизации: с какой частотой брать отсчеты сигнала для того, чтобы была возможность его обратного восстановления по этим отсчетам? Очевидно, что если брать отсчеты слишком редко, то в них не будет содержаться информация о быстро меняющемся сигнале. Скорость изменения сигнала характеризуется верхней частотой его спектра. Таким образом, минимально допустимая ширина интервала дискретизации связана с наибольшей частотой спектра сигнала (обратно пропорциональна ей). Для случая равномерной дискретизации справедлива теорема Котельникова: если непрерывный сигнал x(t) имеет спектр, ограниченный частотой F max, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым с периодом
|
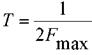, т.е. с частотой 
